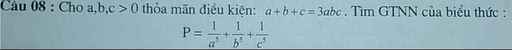Ap dụng bất đẳng thức AM - GM :
\(\dfrac{1}{a^5}+\dfrac{1}{b^5}+1+1+1\ge\dfrac{5}{ab}\left(1\right)\)
\(\dfrac{1}{b^5}+\dfrac{1}{c^5}\ge\dfrac{5}{ab}\left(2\right)\)
\(\dfrac{1}{c^5}+\dfrac{1}{a^5}+1+1+1\ge\dfrac{5}{ab}\left(3\right)\)
Từ (1) , (2) và (3) , cộng theo vế ta có :
\(2P+9\ge5\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)=5.\dfrac{c+a+b}{abc}=15\)
\(\Rightarrow2P\ge6\)
\(\Rightarrow P\ge3\)
Dấu bằng xảy ra khi :
\(\left\{{}\begin{matrix}a,b,c>0\\a+b+c=3abc\\\dfrac{1}{a^5}=\dfrac{1}{b^5}=\dfrac{1}{c^5}=1\end{matrix}\right.\)
Vậy \(P_{min}=3\Rightarrow a=b=c=1\)
Đúng 3
Bình luận (0)
