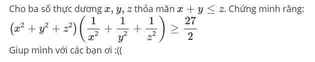\(z\ge x+y\Rightarrow\dfrac{z}{x+y}\ge1\)
\(P\ge\left(\dfrac{1}{2}\left(x+y\right)^2+z^2\right)\left(\dfrac{8}{\left(x+y\right)^2}+\dfrac{1}{z^2}\right)=5+\dfrac{\left(x+y\right)^2}{2z^2}+\dfrac{8z^2}{\left(x+y\right)^2}\)
\(P\ge5+\dfrac{1}{2}\left(\dfrac{x+y}{z}\right)^2+\dfrac{1}{2}\left(\dfrac{z}{x+y}\right)^2+\dfrac{15}{2}\left(\dfrac{z}{x+y}\right)^2\)
\(P\ge5+\dfrac{1}{2}.2\sqrt{\left(\dfrac{x+y}{z}\right)^2\left(\dfrac{z}{x+y}\right)^2}+\dfrac{15}{2}.1^2=\dfrac{27}{2}\)
Dấu "=" xảy ra khi \(2x=2y=z\)
Đúng 1
Bình luận (0)
