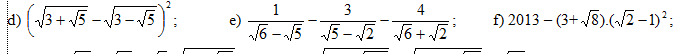\(d,\left(\sqrt{3+\sqrt{5}}-\sqrt{3-\sqrt{5}}\right)=3+\sqrt{5}-2\sqrt{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}+3-\sqrt{5}=6-2\sqrt{4}=6-2.2=6-4=2\)
\(e,\dfrac{1}{\sqrt{6}-\sqrt{5}}-\dfrac{3}{\sqrt{5}-\sqrt{2}}-\dfrac{4}{\sqrt{6}+\sqrt{2}}\\ =\dfrac{\sqrt{6}+\sqrt{5}}{\left(\sqrt{6}-\sqrt{5}\right)\left(\sqrt{6}+\sqrt{5}\right)}-\dfrac{3\left(\sqrt{5}+\sqrt{2}\right)}{\left(\sqrt{5}-\sqrt{2}\right)\left(\sqrt{5}+\sqrt{2}\right)}-\dfrac{4\left(\sqrt{6}-\sqrt{2}\right)}{\left(\sqrt{6}+\sqrt{2}\right)\left(\sqrt{6}-\sqrt{2}\right)}\)
\(=\dfrac{\sqrt{6}+\sqrt{5}}{1}-\dfrac{3\left(\sqrt{5}+\sqrt{2}\right)}{3}-\dfrac{4\left(\sqrt{6}-\sqrt{2}\right)}{4}\)
\(=\sqrt{6}+\sqrt{5}-\left(\sqrt{5}+\sqrt{2}\right)-\left(\sqrt{6}-\sqrt{2}\right)\)
\(=\sqrt{6}+\sqrt{5}-\sqrt{5}-\sqrt{2}-\sqrt{6}+\sqrt{2}\)
\(=0\)