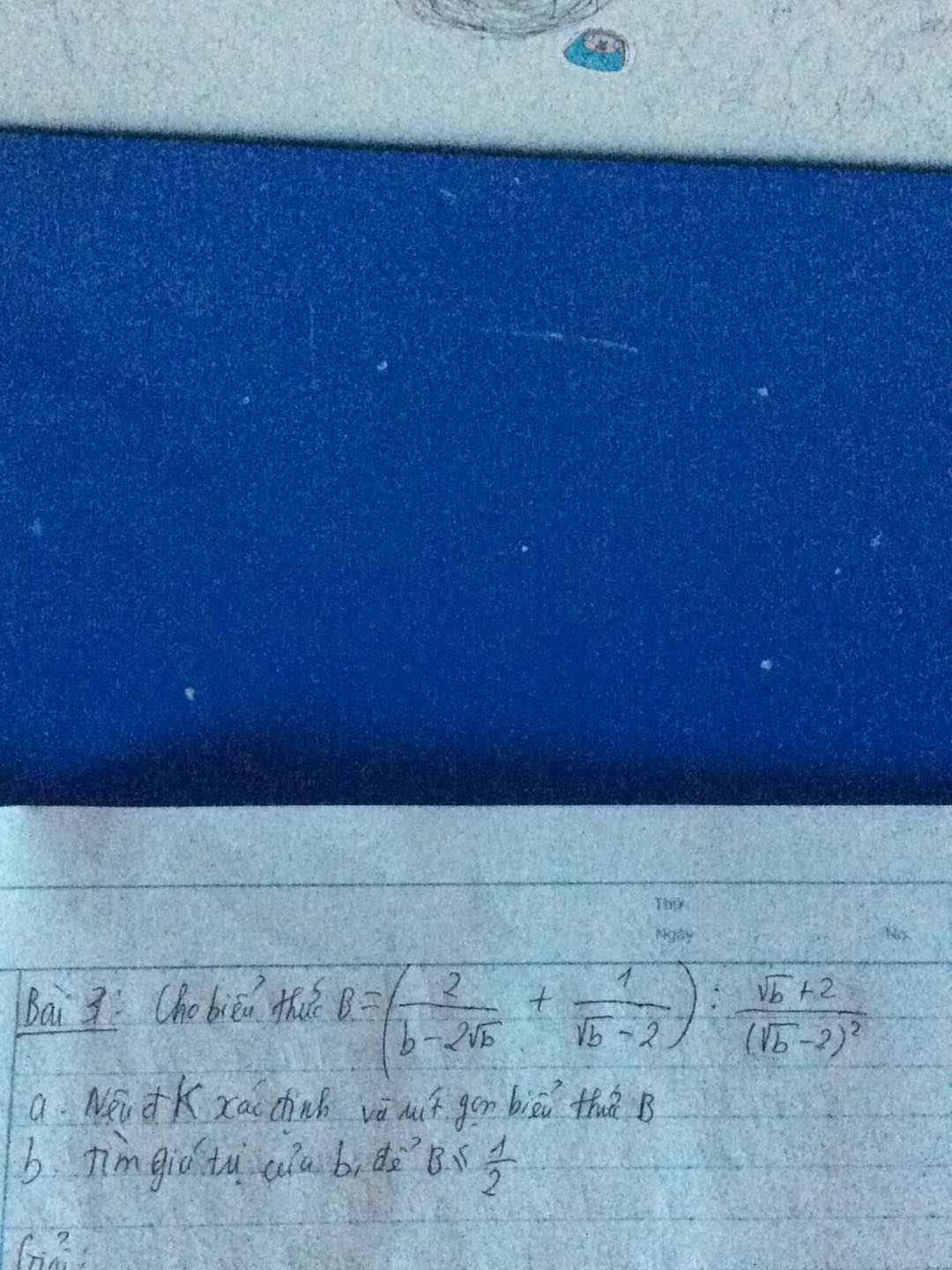a, B = (\(\dfrac{2}{b-2\sqrt{b}}\) + \(\dfrac{1}{\sqrt{b}-2}\)) : \(\dfrac{\sqrt{b}+2}{\left(\sqrt{b}-2\right)^2}\) ĐK: \(\sqrt{b}\ne2\); \(b\ge0\)
<=> \(\dfrac{\sqrt{b}+2}{\sqrt{b}\left(\sqrt{b}-2\right)}\) : \(\dfrac{\sqrt{b}+2}{\left(\sqrt{b}-2\right)^2}\)
<=> \(\dfrac{1}{\sqrt{b}\left(\sqrt{b}-2\right)}\)
b, để B \(\le\) \(\dfrac{1}{2}\)
=> \(\dfrac{1}{\sqrt{b}\left(\sqrt{b}-2\right)}\) \(\le\) \(\dfrac{1}{2}\)
<=> \(\sqrt{b}\left(\sqrt{b}-2\right)\) \(\ge2\)
<=> \(b-2\sqrt{b}\) \(\ge2\)
<=> b - 2 \(\ge\) 2\(\sqrt{b}\)
<=> b2 - 4b + 4 \(\ge\) 4b
<=> (b - 4 - \(2\sqrt{3}\)).(b - 4 + \(2\sqrt{3}\)) \(\ge\) 0
=> để B \(\le\) \(\dfrac{1}{2}\) => b \(\ge4+2\sqrt{3}\)