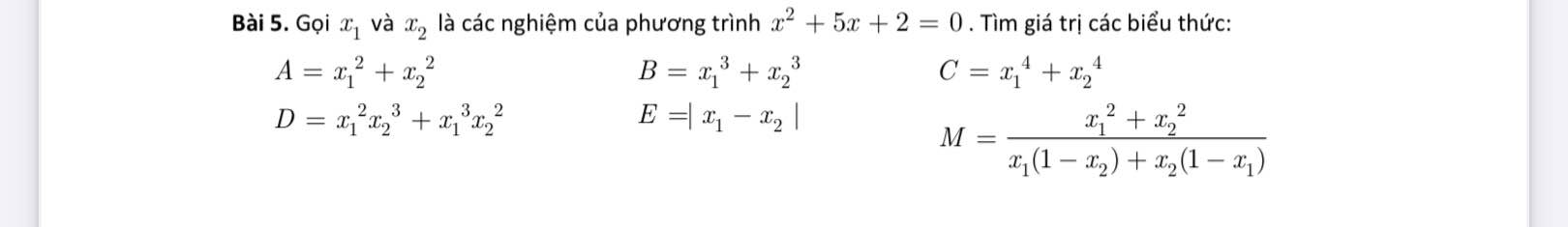Bài 5:
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=-5\\x_1x_2=2\end{matrix}\right.\)
\(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=25-4=21\\ B=x_1^3+x_2^3=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=-125+3\cdot5\cdot2=-95\\ C=x_1^4+x_2^4=\left(x_1^2+x_2^2\right)^2-2x_1^2x_2^2=21^2-2\left(x_1x_2\right)^2=441-2\cdot2^2=433\\ D=x_1^2x_2^3+x_1^3x_2^2=x_1^2x_2^2\left(x_1+x_2\right)=4\left(-5\right)=-20\\ E=\left|x_1-x_2\right|=\sqrt{\left(x_1-x_2\right)^2}=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\\ E=\sqrt{25-8}=\sqrt{17}\\ M=\dfrac{x_1^2+x_2^2}{x_1-x_1x_2+x_2-x_1x_2}=\dfrac{21}{-5-2\cdot2}=-\dfrac{21}{9}\)
Đúng 1
Bình luận (0)
