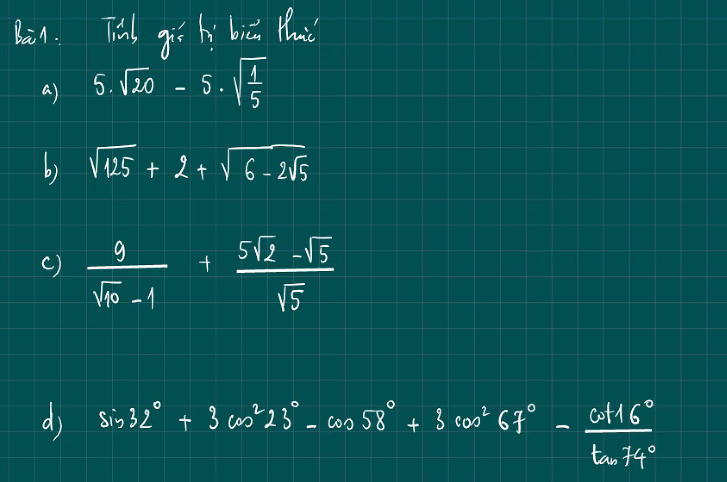Question

Answer 1

\(a,=10\sqrt{5}-\sqrt{5}=9\sqrt{5}\\ b,=5\sqrt{5}+2+\sqrt{\left(\sqrt{5}-1\right)^2}=5\sqrt{5}+2+\sqrt{5}-1=6\sqrt{5}+1\\ c,=\dfrac{9\left(\sqrt{10}+1\right)}{9}+\dfrac{\sqrt{5}\left(\sqrt{10}-1\right)}{\sqrt{5}}=\sqrt{10}+1+\sqrt{10}-1=2\sqrt{10}\\ d,=\left(\sin32^0-\sin32^0\right)+3\left(\sin^267^0+\cos^267^0\right)-\dfrac{\tan74^0}{\tan74^0}=0+3\cdot1-1=2\)

Answer 2

c: \(=\sqrt{10}+1+\sqrt{10}-1=2\sqrt{10}\)