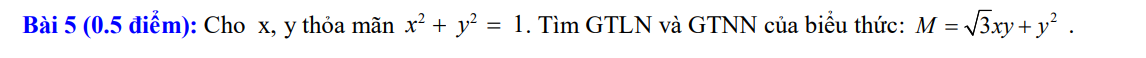Lời giải:
Tìm max
Áp dụng BĐT Cô-si:
$\sqrt{3}xy\leq \frac{3x^2+y^2}{2}$
$\Rightarrow M=\sqrt{3}xy+y^2\leq \frac{3x^2+y^2}{2}+y^2=\frac{3}{2}(x^2+y^2)=\frac{3}{2}$
Vậy $y_{\max}=\frac{3}{2}$ khi $(x,y)=(\frac{\pm 1}{2}, \frac{\pm \sqrt{3}}{2})$
--------------
Tìm min
$(x+\sqrt{3}y)^2\geq 0$
$\Rightarrow \sqrt{3}xy\geq \frac{-x^2-3y^2}{2}$
$\Rightarrow M\geq \frac{-x^2-y^2}{2}=\frac{-1}{2}$
Vậy $M_{\min}=\frac{-1}{2}$ khi $(x,y)=(\frac{-\sqrt{3}}{2}; \frac{1}{2})$