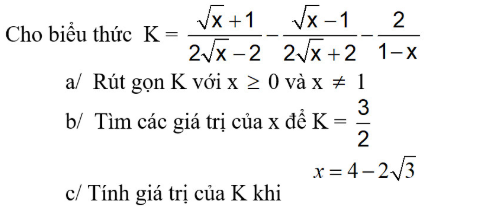\(a,K=\dfrac{\left(\sqrt{x}+1\right)^2-\left(\sqrt{x}-1\right)^2+4}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ K=\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1+4}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ K=\dfrac{4\left(\sqrt{x}+1\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2}{\sqrt{x}-1}\)
\(b,K=\dfrac{3}{2}\Leftrightarrow\dfrac{2}{\sqrt{x}-1}=\dfrac{3}{2}\Leftrightarrow3\sqrt{x}-3=4\\ \Leftrightarrow\sqrt{x}=\dfrac{7}{3}\Leftrightarrow x=\dfrac{49}{9}\)
\(c,x=4-2\sqrt{3}\Leftrightarrow\sqrt{x}=\sqrt{3}-1\\ \Leftrightarrow K=\dfrac{2}{\sqrt{3}-1-1}=\dfrac{2}{\sqrt{3}-2}=\dfrac{2\left(\sqrt{3}+2\right)}{-1}=-2\sqrt{3}-4\)