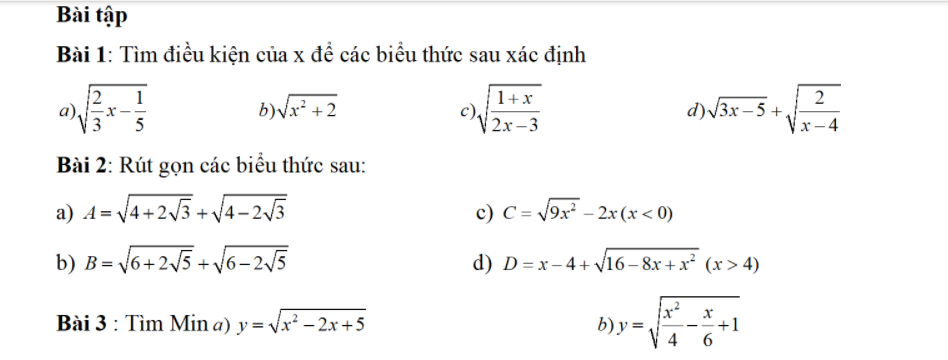\(1,\\ a,ĐK:\dfrac{2}{3}x-\dfrac{1}{5}\ge0\Leftrightarrow x\ge\dfrac{1}{5}\cdot\dfrac{3}{2}=\dfrac{3}{10}\\ b,ĐK:x^2+2\ge0\Leftrightarrow x\in R\left(x^2+2\ge2>0\right)\\ c,ĐK:\dfrac{1+x}{2x-3}\ge0\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}1+x\ge0\\2x-3>0\end{matrix}\right.\\\left\{{}\begin{matrix}1+x\le0\\2x-3< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge-1\\x>\dfrac{3}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}x\le-1\\x< \dfrac{3}{2}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>\dfrac{3}{2}\\x\le-1\end{matrix}\right.\)
\(d,ĐK:\left\{{}\begin{matrix}3x-5\ge0\\\dfrac{2}{x-4}\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{5}{3}\\x-4\ge0\left(2>0\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{5}{3}\\x\ge4\end{matrix}\right.\Leftrightarrow x\ge4\)
\(2,\\ a,A=\sqrt{\left(\sqrt{3}+1\right)^2}+\sqrt{\left(\sqrt{3}-1\right)^2}=\sqrt{3}+1+\sqrt{3}-1=2\sqrt{3}\\ b,B=\sqrt{\left(\sqrt{5}+1\right)^2}+\sqrt{\left(\sqrt{5}-1\right)^2}=\sqrt{5}+1+\sqrt{5}-1=2\sqrt{5}\\ c,C=\left|3x\right|-2x=-3x-2x=-5x\\ d,D=x-4+\sqrt{\left(x-4\right)^2}=x-4+\left|x-4\right|=x-4+x-4=2x-8\)
\(3,\\ a,y=\sqrt{x^2-2x+5}=\sqrt{\left(x-1\right)^2+4}\ge\sqrt{4}=2\)
Dấu \("="\Leftrightarrow x=1\)
\(b,y=\sqrt{\dfrac{x^2}{4}-\dfrac{x}{6}+1}=\sqrt{\dfrac{x^2}{4}-2\cdot\dfrac{1}{2}\cdot\dfrac{1}{6}x+\dfrac{1}{36}+\dfrac{35}{36}}\\ =\sqrt{\left(\dfrac{x}{2}-\dfrac{1}{6}\right)^2+\dfrac{35}{36}}\ge\sqrt{\dfrac{35}{36}}=\dfrac{\sqrt{35}}{6}\)
Dấu \("="\Leftrightarrow6x=2\Leftrightarrow x=\dfrac{1}{3}\)
bài 1
a)\(\dfrac{2}{3}x-\dfrac{1}{5}\ge0\Rightarrow\dfrac{2}{3}x\ge\dfrac{1}{5}\Rightarrow x\ge0,3\)
b)ta có:2>0 vậy \(x^2+2>0\forall x\)
c)\(\dfrac{1+x}{2x-3}\ge0\Leftrightarrow\left[{}\begin{matrix}1+x\ge0\\2x-3\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge-1\\x\ne\dfrac{3}{2}\end{matrix}\right.\)
d)\(\left[{}\begin{matrix}3x-5\ge0\\x-4\ne0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\ge\dfrac{5}{3}\\x\ne4\end{matrix}\right.\)
bài2
a) ta có:\(A^2=\left(\sqrt{4+2\sqrt{3}}+\sqrt{4-2\sqrt{3}}\right)^2\)
=\(4+2\sqrt{3}+4-2\sqrt{3}+2\sqrt{\left(4+2\sqrt{3}\right)\left(4-2\sqrt{3}\right)}\)
=\(8+2\sqrt{4}=8+4=12\)
\(\Rightarrow A=\pm\sqrt{12}\) mà A>0 nên A=\(\sqrt{12}\)
b)ta có:\(B^2=\left(\sqrt{6+2\sqrt{5}}+\sqrt{6-2\sqrt{5}}\right)^2\)
=\(6+2\sqrt{5}+6-2\sqrt{5}+2\sqrt{\left(6+2\sqrt{5}\right)\left(6-2\sqrt{5}\right)}\)
=\(12+2\sqrt{16}=12+8=20\)
\(\Rightarrow B=\pm\sqrt{20}\) mà B>0 nên B=\(\sqrt{20}\)
c)C=\(\left|3x\right|-2x=-3x-2x=-5x\left(\forall x< 0\right)\)
d)D=\(x-4+\sqrt{\left(4-x\right)^2}=x-4+\left|4-x\right|\)
=x-4+x-4=2x-8
bài 3
a)y=\(\sqrt{x^2-2x+1+4}=\sqrt{\left(x-1\right)^2+4}\)
ta có:\(\left(x-1\right)^2\ge0\Rightarrow\left(x-1\right)^2+4\ge4\)\(\Rightarrow\sqrt{\left(x-1\right)^2+4}\ge\sqrt{4}=2\)
vậy Miny=2 khi x=1
b)y=\(\sqrt{\dfrac{x^2}{4}-\dfrac{x}{6}+\dfrac{1}{36}+\dfrac{35}{36}}\)=\(\sqrt{\left(\dfrac{x}{2}-\dfrac{1}{6}\right)^2+\dfrac{35}{36}}\)
ta có:\(\left(\dfrac{x}{2}-\dfrac{1}{6}\right)^2\ge0\Rightarrow\left(\dfrac{x}{2}-\dfrac{1}{6}\right)^2+\dfrac{35}{36}\ge\dfrac{35}{36}\)
\(\Rightarrow\sqrt{\left(\dfrac{x}{2}-\dfrac{1}{6}\right)^2+\dfrac{35}{36}}\ge\dfrac{\sqrt{35}}{6}\)
vậy Miny=\(\dfrac{\sqrt{35}}{6}\)khi x=\(\dfrac{1}{3}\)