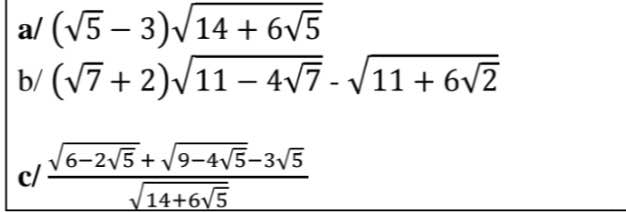a) \(\left(\sqrt{5}-3\right)\sqrt{14+6\sqrt{5}}=\left(\sqrt{5}-3\right)\sqrt{\left(\sqrt{5}+3\right)^2}=\left(\sqrt{5}-3\right)\left(\sqrt[]{5}+3\right)=25-9=16\)
b) \(\left(\sqrt{7}+2\right)\sqrt{11-4\sqrt{7}}-\sqrt{11+6\sqrt{2}}=\left(\sqrt{7}+2\right)\sqrt{\left(\sqrt{7}-2\right)^2}-\sqrt{\left(3-\sqrt{2}\right)^2}=\left(\sqrt{7}+2\right)\left(\sqrt{7}-2\right)-\left(3-\sqrt{2}\right)=7-4-3+\sqrt{2}=\sqrt{2}\)
c) \(\dfrac{\sqrt{6-2\sqrt{5}}+\sqrt{9-4\sqrt{5}}-3\sqrt{5}}{\sqrt{14+6\sqrt{5}}}=\dfrac{\sqrt{\left(\sqrt{5}-1\right)^2}+\sqrt{\left(\sqrt{5}-2\right)^2}-3\sqrt{5}}{\sqrt{\left(3+\sqrt{5}\right)^2}}=\dfrac{\sqrt{5}-1+\sqrt{5}-2-3\sqrt{5}}{3+\sqrt{5}}=\dfrac{-3-\sqrt{5}}{3+\sqrt{5}}=-1\)