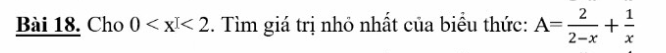ap dung BDT AM-GM \(\Rightarrow A=\dfrac{2}{2-x}+\dfrac{1}{x}\ge\dfrac{\left(\sqrt{2}+1\right)^2}{2-x+x}=\dfrac{3+2\sqrt{2}}{2}\)
\(\Rightarrow Amin=\dfrac{3+2\sqrt{2}}{2}\)
Vì 0 < x < 2 nên x = 1 ( * ) .
Ta có :
A = \(\dfrac{2}{2-x}\) + \(\dfrac{1}{x}\) .
\(\rightarrow\) Thế ( * ) :
\(\Leftrightarrow\) A = \(\dfrac{2}{2-1}\) + \(\dfrac{1}{1}\) .
\(\Leftrightarrow\) A = 2 + 1 .
\(\Leftrightarrow\) A = 3 .
Vậy giá trị nhỏ nhất của biểu thức là : 3