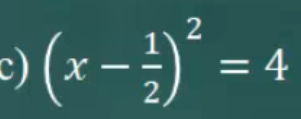Question

Answer 1

c: Ta có: \(\left(x-\dfrac{1}{2}\right)^2=4\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{1}{2}=2\\x-\dfrac{1}{2}=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)

Answer 2

\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{1}{2}=2\\x-\dfrac{1}{2}=-2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)

Answer 3

\(\left(x-\dfrac{1}{2}\right)^2=4\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{1}{2}=2\\x-\dfrac{1}{2}=-2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)

Answer 4

\(\left(x-\dfrac{1}{2}\right)^2=2^2\)

\(x-\dfrac{1}{2}=2\)

\(x=\dfrac{5}{2}\)

Answer 5

TH1:x-1/2=4 =>x=9/8

Th2:x-1/2=-4 =>x=-7/8

Answer 6

\(\left(x-\dfrac{1}{2}\right)^2=4\)

<=> \(\left(x-\dfrac{1}{2}\right)^2-2^2=0\)

<=> \(\left(x-\dfrac{1}{2}-2\right)\left(x-\dfrac{1}{2}+2\right)=0\)

<=> \(\left[{}\begin{matrix}x-\dfrac{1}{2}-2=0\\x-\dfrac{1}{2}+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)