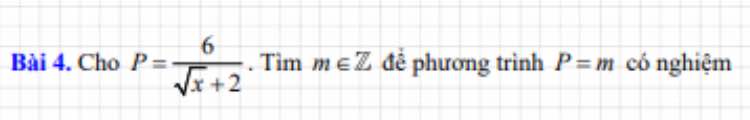Question

Answer 1

Đk x≥0 

xét pt \(\dfrac{6}{\sqrt{x}+2}=m\)

=>\(\sqrt{x}+2=\dfrac{6}{m}\)

\(< =>\sqrt{x}=\dfrac{6}{m}-2\)

để pt 1 có nghiệm x thì pt 2 cx có nghiệm x 

=> \(\dfrac{6-2m}{m}\text{≥}0\)

=> 6-2m≥0 => m ≤ 3 , m>0

hoặc 6-2m ≤ 0 => 3≤m,m<0 ( vô lý)

vậy 0<m≤3 thì pt p=m có nghiệm

Answer 2

Để P nguyên thì \(\sqrt{x}+2\in\left\{2;3;6\right\}\)

hay \(x\in\left\{0;1;16\right\}\)

\(\Leftrightarrow m\in\left\{3;2;1\right\}\)