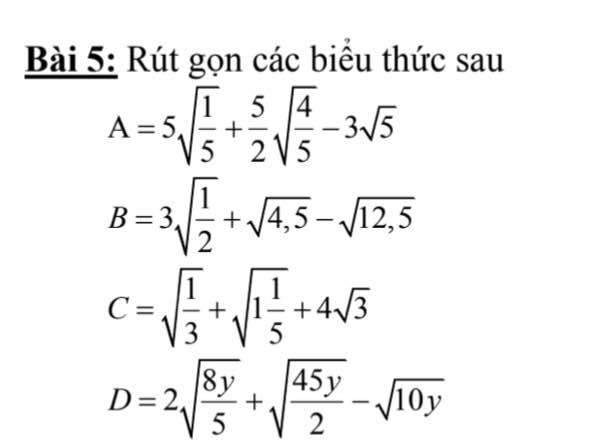$A=5\sqrt{\dfrac{1}{5}}+\dfrac{5}{2}\sqrt{\dfrac{4}{5}}-3\sqrt 5\\=(\sqrt 5)^2.\dfrac{1}{\sqrt 5}+\dfrac{(\sqrt 5)^2}{2}.\dfrac{2}{\sqrt 5}-3\sqrt 5\\=\sqrt 5+\sqrt 5-3\sqrt 5\\=-\sqrt 5$
Vậy $A=-\sqrt 5$
\(B=3\sqrt{\dfrac{1}{2}}+\sqrt{4,5}-\sqrt{12,5}=\dfrac{3\sqrt{2}}{2}+\dfrac{3\sqrt{2}}{2}-\dfrac{5\sqrt{2}}{2}=\dfrac{\sqrt{2}}{2}\)
\(C=\sqrt{\dfrac{1}{3}}+\sqrt{1\dfrac{1}{5}}+4\sqrt{3}=\dfrac{\sqrt{3}}{3}+\dfrac{\sqrt{30}}{5}+4\sqrt{3}=\dfrac{5\sqrt{3}+3\sqrt{30}+4\sqrt{3}}{15}=\dfrac{9\sqrt{3}+3\sqrt{30}}{15}=\dfrac{\sqrt{30}+3\sqrt{3}}{5}\)\(D=2\sqrt{\dfrac{8y}{5}}+\sqrt{\dfrac{45y}{2}}-\sqrt{10y}=\dfrac{20\sqrt{2y}}{5}+\dfrac{3\sqrt{10y}}{2}-\sqrt{10y}=\dfrac{40\sqrt{2y}+15\sqrt{10y}-10\sqrt{10y}}{10}=\dfrac{40\sqrt{2y}+5\sqrt{10y}}{10}=\dfrac{8\sqrt{2y}+\sqrt{10y}}{2}\)