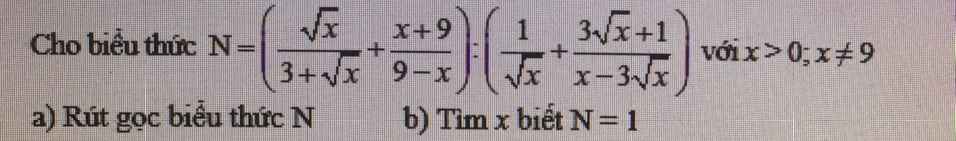a) \(N=\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{x+9}{9-x}\right):\left(\dfrac{1}{\sqrt{x}}+\dfrac{3\sqrt{x}+1}{x-3\sqrt{x}}\right)\)
\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{x+9}{\left(3-\sqrt{x}\right)\left(\sqrt{x}+3\right)}\right):\left(\dfrac{1}{\sqrt{x}}+\dfrac{3\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-3\right)}\right)\)
\(=\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)+x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}:\dfrac{\sqrt{x}-3+3\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3\sqrt{x}+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}:\dfrac{4\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3\left(\sqrt{x}+3\right)}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{4\sqrt{x}-2}=\dfrac{-3\sqrt{x}}{4\sqrt{x}-2}=\dfrac{3\sqrt{x}}{2-4\sqrt{x}}\)
b) \(N=1\Rightarrow\dfrac{3\sqrt{x}}{2-4\sqrt{x}}=1\Rightarrow3\sqrt{x}=2-4\sqrt{x}\Rightarrow7\sqrt{x}=2\)
\(\Rightarrow\sqrt{x}=\dfrac{2}{7}\Rightarrow x=\dfrac{4}{49}\)