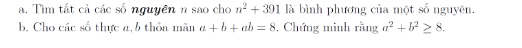Question

Answer 1

a.

Đặt \(n^2+391=k^2\) với \(k\in Z\)

\(\Rightarrow k^2-n^2=391\)

\(\Rightarrow\left(k-n\right)\left(k+n\right)=391\)

k-n	391	-391	1	-1	17	-17	23	-23
k+n	1	-1	391	-391	23	-23	17	-17
n	-195	195	195	-195	3	-3	-3	3

 

Vậy \(n=\left\{\pm195;\pm3\right\}\)

 

Answer 2

b.

Với mọi số thực a; b ta luôn có:

\(2\left(a-b\right)^2+\left(a-2\right)^2+\left(b-2\right)^2\ge0\)

\(\Leftrightarrow2a^2-4ab+2b^2+a^2-4a+4+b^2-4b+4\ge0\)

\(\Leftrightarrow3\left(a^2+b^2\right)+8\ge4\left(a+b+ab\right)\)

\(\Leftrightarrow3\left(a^2+b^2\right)+8\ge32\)

\(\Leftrightarrow3\left(a^2+b^2\right)\ge24\)

\(\Rightarrow a^2+b^2\ge8\) (đpcm)

Dấu "=" xảy ra khi \(a=b=2\)