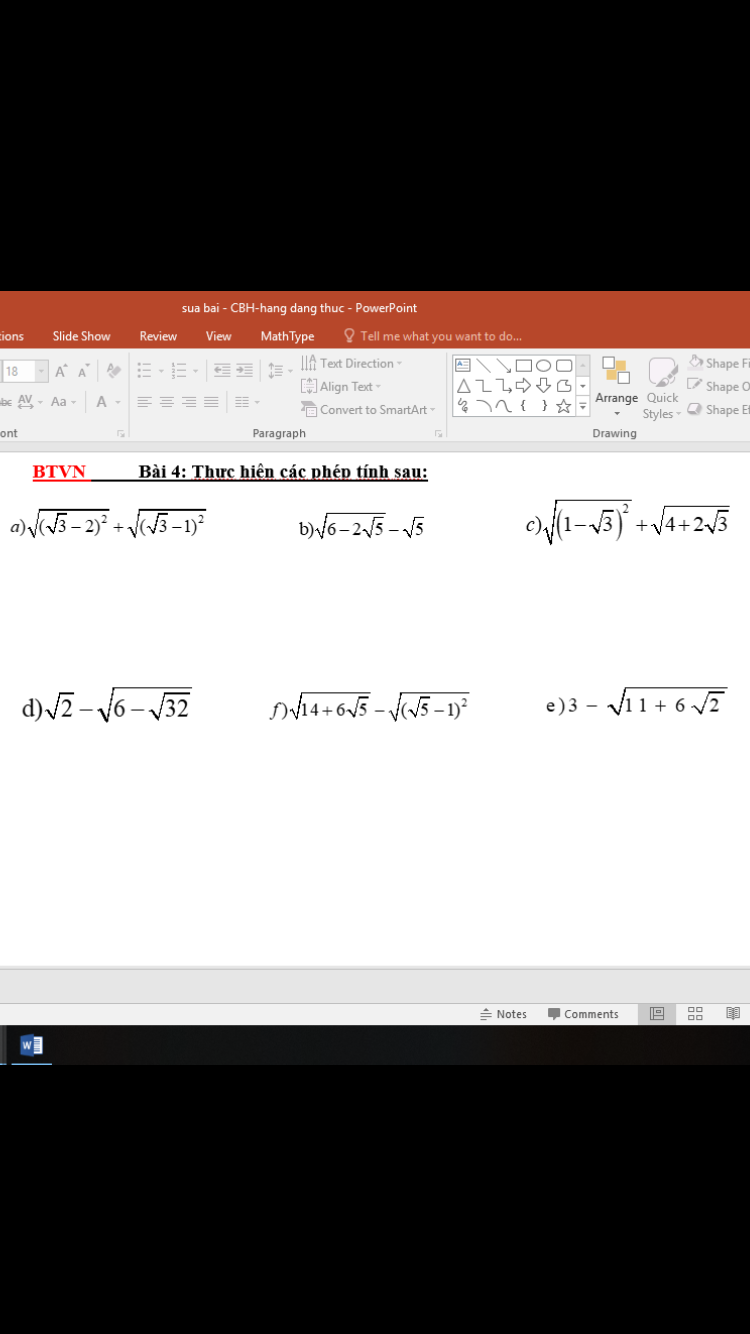
a) \(\sqrt{\left(\sqrt{3}-2\right)^2}+\sqrt{\left(\sqrt{3}-1\right)^2}\)
\(=2-\sqrt{3}+\sqrt{3}-1\)
=1
b) \(\sqrt{6-2\sqrt{5}}-\sqrt{5}\)
\(=\sqrt{5}-1-\sqrt{5}\)
=-1
c) \(\sqrt{\left(1-\sqrt{3}\right)^2}+\sqrt{4+2\sqrt{3}}\)
\(=\sqrt{3}-1+\sqrt{3}+1\)
\(=2\sqrt{3}\)
d) \(\sqrt{2}-\sqrt{6-\sqrt{32}}\)
\(=\sqrt{2}-2+\sqrt{2}\)
\(=2\sqrt{2}-2\)
e) \(\sqrt{14+6\sqrt{5}}-\sqrt{\left(\sqrt{5}-1\right)^2}\)
\(=3+\sqrt{5}-\sqrt{5}+1\)
=4
f) \(3-\sqrt{11+6\sqrt{2}}\)
\(=3-3-\sqrt{2}\)
\(=-\sqrt{2}\)
a, \(\sqrt{\left(\sqrt{3}-2\right)^2}+\sqrt{\left(\sqrt{3}-1\right)^2}=2-\sqrt{3}+\sqrt{3}-1=1\)
b, \(\sqrt{6-2\sqrt{5}}-\sqrt{5}=\sqrt{\left(\sqrt{5}-1\right)^2}-\sqrt{5}=\sqrt{5}-1-\sqrt{5}=-1\)
c, \(\sqrt{\left(1-\sqrt{3}\right)^2}+\sqrt{4+2\sqrt{3}}=\sqrt{3}-1+\sqrt{\left(\sqrt{3}+1\right)^2}\)
\(=\sqrt{3}-1+\sqrt{3}+1=2\sqrt{3}\)
d, \(\sqrt{2}-\sqrt{6-\sqrt{32}}=\sqrt{2}-\sqrt{6-2\sqrt{4.2}}\)
\(=\sqrt{2}-\sqrt{\left(\sqrt{4}-\sqrt{2}\right)^2}=\sqrt{2}-\sqrt{4}+\sqrt{2}=2\sqrt{2}-\sqrt{4}\)
f, \(\sqrt{14+6\sqrt{5}}-\sqrt{\left(\sqrt{5}-1\right)^2}=\sqrt{\left(3+\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{5}-1\right)^2}\)
\(=3+\sqrt{5}-\sqrt{5}+1=4\)
e, \(3-\sqrt{11+6\sqrt{2}}=3-\sqrt{\left(3+\sqrt{2}\right)^2}=3-3-\sqrt{2}=-\sqrt{2}\)