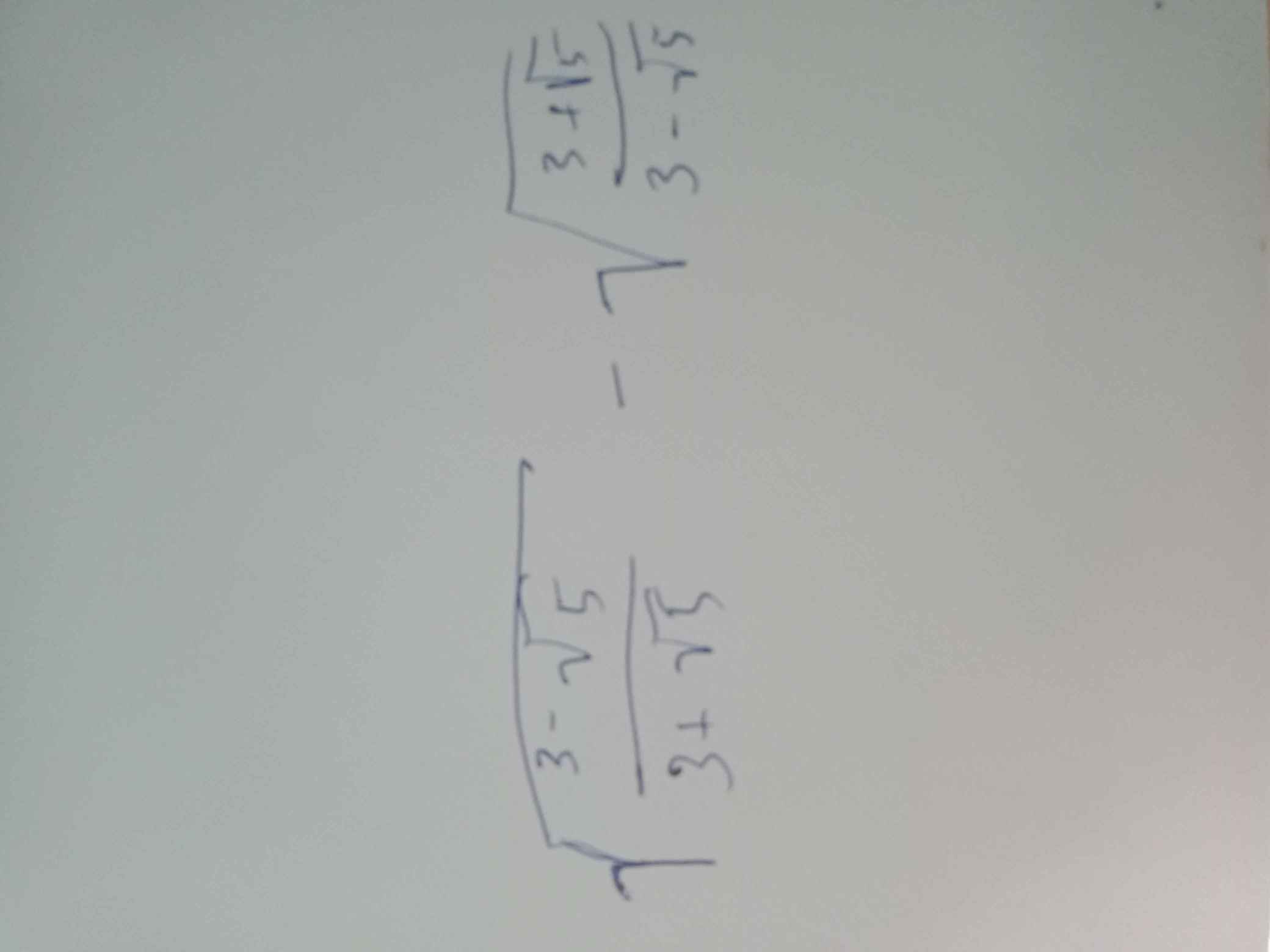
\(\sqrt{\dfrac{3-\sqrt{5}}{3+\sqrt{5}}}-\sqrt{\dfrac{3+\sqrt{5}}{3-\sqrt{5}}}\)\(=\sqrt{\dfrac{6-2\sqrt{5}}{6+2\sqrt{5}}}-\sqrt{\dfrac{6+2\sqrt{5}}{6-2\sqrt{5}}}\)
\(=\sqrt{\dfrac{\left(\sqrt{5}-1\right)^2}{\left(\sqrt{5}+1\right)^2}}-\sqrt{\dfrac{\left(\sqrt{5}+1\right)^2}{\left(\sqrt{5}-1\right)^2}}\)
\(=\dfrac{\left|\sqrt{5}-1\right|}{\sqrt{5}+1}-\dfrac{\sqrt{5}+1}{\left|\sqrt{5}-1\right|}\)
\(=\dfrac{\sqrt{5}-1}{\sqrt{5}+1}-\dfrac{\sqrt{5}+1}{\sqrt{5}-1}=\dfrac{\left(\sqrt{5}-1\right)^2-\left(\sqrt{5}+1\right)^2}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}=-\dfrac{4\sqrt{5}}{4}\)\(=-\sqrt{5}\)
Vậy...
Đúng 2
Bình luận (0)
