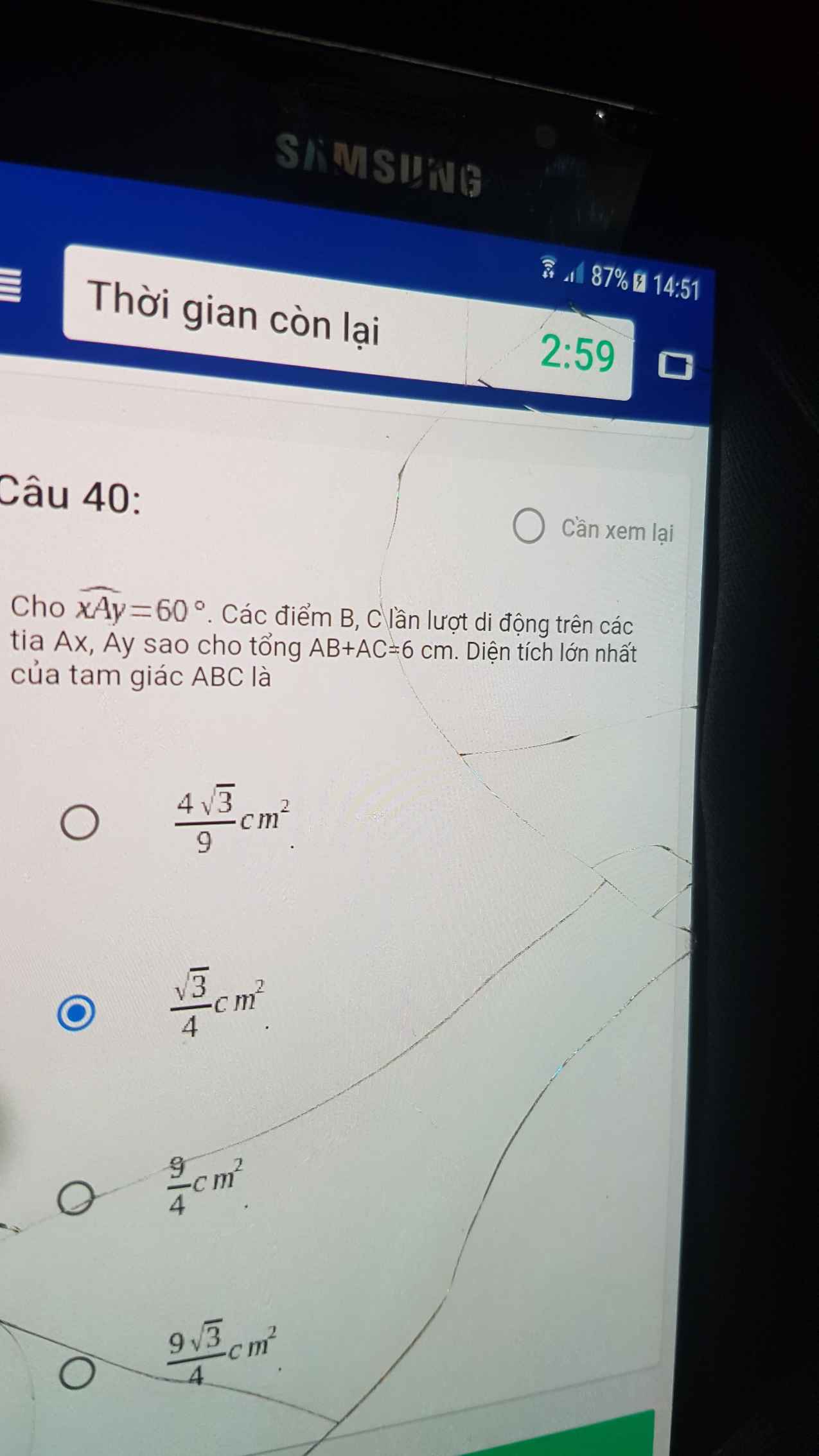
Ta chứng minh công thức sau: \(S_{ABC}=\dfrac{1}{2}.sinA.AB.AC\)
Kẻ \(BF\perp AC\)\(\Rightarrow sinA=\dfrac{BF}{AB}\)
Có \(S_{ABC}=\dfrac{1}{2}.BF.AC=\dfrac{1}{2}.AC.AB.sinA\) (đpcm)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}.sin60^0.AB.AC=\dfrac{\sqrt{3}}{4}.AB.AC\)\(\le\dfrac{\sqrt{3}}{4}.\left(\dfrac{AB+AC}{2}\right)^2=\dfrac{9\sqrt{3}}{4}\) (cm2) (Theo bđt AM-MG với hai số dương)
Dấu = xảy ra khi AB=AC=3 (cm)
Vậy \(S_{max}=\dfrac{9\sqrt{3}}{4}\) cm2