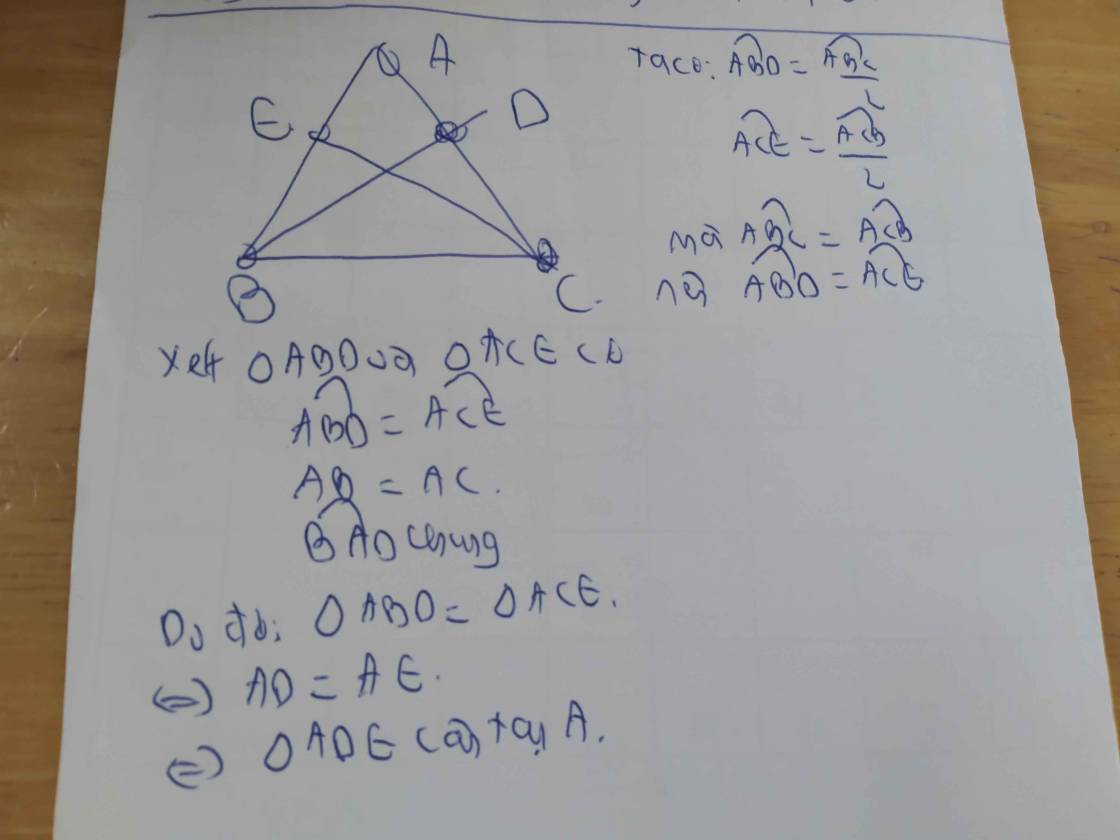
cho tam giác abc cân tại a tia pg góc b cắt mạnh ac tại dtia pg góc c cắt mạnh ab tại e . cm ade cân
Bài 6: Tam giác cân
CHO ΔABC CÓ AB= AC VÀ AB≥ BC GỌI M LÀ TRUNG ĐIỂM CỦA CẠNH BC A/ CHỨNG MINH Δ ABM = Δ ACM VÀ AM VUÔNG BC B/ TRÊN CẠNH AB LẤY ĐIỂM D TRÊN CẠNH AC LẤY ĐIỂM E SAO CHO AD = AE CHỨNG MINH Δ MDE CÂN
cho Δ ABC cân tại A lấy điểm D thuộc cạnh AC điểm E thuộc cạnh AB sao cho AD = AE A/ SO sánh ABD = ACE B/ Gọi I là giao điểm của BD và CE Tam giác IBC là tam giác gì vì sao ? C/ chứng minh ED//BC
kẻ bd vuông ac . ce vuong ab d thuộc ac , e thuộc ab chứng minh be= cd
cho tam giác ABC cân tại A .Tính góc B
Đề chưa đủ dữ kiện đâu em
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Gọi M, N là trung điểm các cạnh AB, AC. Các đường thẳng vuông góc với AB, AC tại M; N cắt nhau tại điểm O, AO cắt BC tại H. Chứng minh HB=HC và AH vuông góc với BC
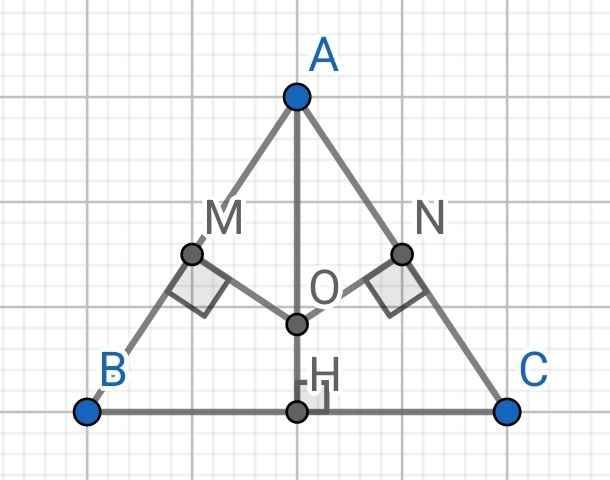
Do OM ⊥ AB (gt)
⇒ OM là đường cao của ∆ABC
Do ON ⊥ AC (gt)
⇒ ON là đường cao của ∆ABC
⇒ O là giao điểm của hai đường cao của ∆ABC
⇒ AO là đường cao thứ ba
⇒ AH ⊥ BC
Xét hai tam giác vuông: ∆ABH và ∆ACH có:
AH là cạnh chung
AB = AC (do ∆ABC cân tại A)
⇒ ∆ABH = ∆ACH (cạnh huyền - cạnh góc vuông)
⇒ HB = HC (hai cạnh tương ứng)
Đúng 1
Bình luận (0)
a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔBAD=ΔBHD
=>BA=BH
b: Ta có: ΔBAD=ΔBHD
=>DA=DH
Ta có: DA=DH
DH<DC(ΔDHC vuông tại H)
Do đó: DA<DC
c: Xét ΔBHI vuông tại H và ΔBAC vuông tại A có
BH=BA
\(\widehat{HBI}\) chung
Do đó: ΔBHI=ΔBAC
=>BI=BC
=>ΔBIC cân tại B
d: Ta có: ΔBHI=ΔBAC
=>HI=AC
Ta có: AD+DC=AC
HD+DI=HI
mà AC=HI và AD=HD
nên DC=DI
=>D nằm trên đường trung trực của CI(1)
ta có: BI=BC
=>B nằm trên đường trung trực của CI(2)
ta có: MI=MC
=>M nằm trên đường trung trực của CI(3)
từ (1),(2),(3) suy ra B,M,D thẳng hàng
Đúng 1
Bình luận (0)
Tam giác ABC có AB=AC và M là trung điểm của BC Trên tia đối của tia MA Lấy điểm k sao cho MK=MA a) vẽ hình,ghi giải thiết, kết luận b) chứng minh tam giác ABM=tam giác ACM c) tam giác ABM=tam giác KCM d) AB // CK Kẻ MH vuông góc AB,MK vuông góc AC Chứng minh MHK cân . Sos mọi người cíu tuii bài này với ạ🙏😿
a:
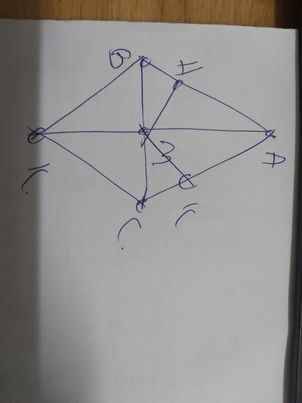
| GT | ΔABC cân tại A M là trung điểm của BC MK=MA MH\(\perp\)AB; MK\(\perp\)AC H\(\in\)AB; K\(\in\)AC |
| KL | b: ΔABM=ΔACM c: ΔABM=ΔKCM d: AB//CK e: MH=MK |
b: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
c: Xét ΔMAB và ΔMKC có
MA=MK
\(\widehat{AMB}=\widehat{KMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMKC
d: Ta có: ΔMAB=ΔMKC
=>\(\widehat{MAB}=\widehat{MKC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//KC
e: ΔAMB=ΔAMC
=>\(\widehat{MAB}=\widehat{MAC}\)
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
=>MH=MK
=>ΔMHK cân tại M
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB=AC, AM là phân giác của góc BAC ( M thuộc BC ):
a, Chứng minh tam giác ABM= tam giác ACM
b, Chứng minh M là trung điểm của BC và AM vuông góc BC
c, Kẻ ME vuông góc AB ( E thuộc AB ) và MF vuông góc AC ( F thuộc AC ). Chứng minh ME=MF
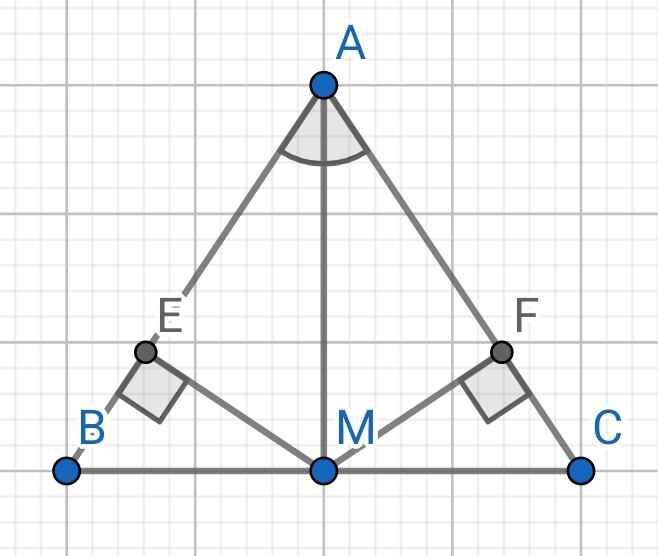 a) Do AM là tia phân giác của ∠BAC (gt)
a) Do AM là tia phân giác của ∠BAC (gt)
⇒ ∠BAM = ∠CAM
Xét ∆ABM và ∆ACM có:
AB = AC (gt)
∠BAM = ∠CAM (cmt)
AM là cạnh chung
⇒ ∆ABM = ∆ACM (c-g-c)
b) Do ∆ABM = ∆ACM (cmt)
⇒ BM = CM (hai cạnh tương ứng)
⇒ M là trung điểm của BC
Do ∆ABM = ∆ACM (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
c) Do ∠BAM = ∠CAM (cmt)
⇒ ∠EAM = ∠FAM
Xét hai tam giác vuông: ∆AME và ∆AMF có:
AM là cạnh chung
∠EAM = ∠FAM (cmt)
⇒ ∆AME = ∆AMF (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng)
Đúng 3
Bình luận (0)
a,
Xét tam giác ABC có:
+ AB = AC (giả thuyết)
+ Góc CAM = MAB (AM là phân giác góc BAC)
+ AM chung
⇒ 2 tam giác bằng nhau (cgc) (đpcm)
b,
Ta có:
+ Tam giác AMC = Tam giác ABM (theo câu a)
⇒ CM = MB (2 cạnh tương ứng) (1)
⇒ M là trung điểm BC (đpcm)
+ Mà AM là tia phân giác góc CAB (2)
+ Góc AMC = Góc AMB (3)
Từ (1), (2), (3).
⇒ AM ⊥ BC (t/c) (đpcm)
c,
Ta có:
Tam giác ACM = Tam giác ABM (theo câu A)
⇒ Góc ACM = Góc ABM (2 góc tương ứng)
Ta có:
+ ME ⊥ AB (giả thuyết)
⇒ Tam giác MEB vuông tại E
+ MF ⊥ AC (giả thuyết)
⇒ Tam giác CFM vuông tại F
Xét tam giác CFM vuông tại F và tam giác MEB vuông tại E có:
+ Góc ACM bằng góc ABM (chứng minh trên)
+ MC = MB (theo câu b)
⇒ Hai tam giác CFM = MEB (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng) (đpcm)
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB=AC, AM là phân giác của góc BAC ( M thuộc BC ):
a, Chứng minh tam giác ABM= tam giác ACM
b, Chứng minh M là trung điểm của BC và AM vuông góc BC
c, Kẻ MF vuông góc AB ( F thuộc AB ) và ME vuông góc AC ( E thuộc AC ). Chứng minh EF // BC
Cho △ABC có AB = AC, AM là phân giác của ∠BAC (M ∈ BC):
a, Chứng minh △ABM = △ACM.
b, Chứng minh M là trung điểm của BC và AM ⊥ BC.
c, Kẻ MF ⊥ AB (F ∈ AB) và ME ⊥ AC (E ∈ AC). Chứng minh EF // BC.
Giải:
a,
- Xét 2 △ABM và △ACM, có:
AB = AC (theo giả thiết)
∠CAM = ∠BAM (AM là phân giác của ∠BAC)
AM_cạnh chung
=> △ABM = △ACM (c.g.c)
b,
- Có △ABM = △ACM (chứng minh trên)
=> MC = MB (2 cạnh tương ứng)
=> M là trung điểm của BC
=> ∠AMC = ∠AMB (2 góc tương ứng)
mà 2 ∠AMC và ∠AMB kề bù
=> ∠AMC = ∠AMB = \(\dfrac{180^o}{2}\) = 90o
<=> AM ⊥ BC
c,
- Xét 2 △AEM và △AFM, có:
∠AEM = ∠AFM = 90o
AM_cạnh chung
∠EAM = ∠FAM (AM là phân giác của ∠EAF)
=> △AEM = △AFM (cạnh huyền - góc nhọn)
=> AE = AF (2 cạnh tương ứng)
<=> △AEF cân tại A
=> ∠AEF = \(\dfrac{180^o-\text{∠}EAF}{2}\) (số đo của một góc ở đáy trong △AEF cân tại A) (1)
Có △ABC cân tại A (AB = AC)
=> ∠ACB = \(\dfrac{180^o-\text{∠}BAC}{2}\) (số đo của một góc ở đáy trong ΔABC cân tại A) (2)
Từ (1) và (2) suy ra ∠AEF = ∠ACB
mà ∠AEF và ∠ACB ở vị trí đồng vị
=> EF//BC
Đúng 1
Bình luận (0)