Em hãy lập kế hoạch cá nhân cho 1 tuần nghỉ TẾT

Em hãy lập kế hoạch cá nhân cho 1 tuần nghỉ TẾT

Dọn dẹp và trang trí nhà cửa
-Trong những ngày đầu tuần nghỉ Tết, em sẽ cùng gia đình dọn dẹp sạch sẽ từng góc nhà. Sau đó, em sẽ phụ mẹ trang trí nhà cửa bằng cách treo câu đối, bày mâm ngũ quả và đặt thêm hoa mai, hoa đào để không gian tràn ngập không khí Tết. Công việc này không chỉ giúp ngôi nhà đẹp hơn mà còn mang lại cảm giác ấm cúng, sẵn sàng đón năm mới.
Đi mua sắm và chuẩn bị thực phẩm Tết
-Giữa tuần, em sẽ theo mẹ đi chợ Tết để mua sắm các nguyên liệu cần thiết như bánh chưng, thịt, và hoa quả
- Em muốn tự chọn một vài món bánh kẹo để đãi khách khứa, bạn bè khi họ đến chơi
-Ngoài ra, em sẽ cùng gia đình chuẩn bị một bữa cơm tất niên ấm cúng, đầy đủ các món ngon
Thăm hỏi và chúc Tết họ hàng
-Trong những ngày đầu năm mới, em sẽ đi thăm ông bà, cô bác và họ hàng
- Em sẽ chúc Tết mọi người bằng những lời chúc ý nghĩa và nhận lì xì may mắn. Những buổi gặp gỡ này không chỉ giúp kết nối tình thân mà còn là dịp để em thể hiện sự biết ơn đối với người lớn trong gia đình.
Gặp gỡ bạn bè và vui chơi
-Bên cạnh việc thăm hỏi họ hàng, hàng xóm -em dự định dành một buổi để tụ tập bạn bè, Đây là dịp để em thư giãn, tạo thêm kỷ niệm đẹp và tận hưởng khoảng thời gian nghỉ ngơi cùng bạn bè.
Học tập và chuẩn bị cho kỳ học mới
-Cuối tuần, em sẽ dành thời gian để ôn bài và hoàn thành những bài tập còn dang dở
- Em lập kế hoạch học tập cho năm mới, đặc biệt tập trung vào môn Toán để cải thiện kết quả học tập
Dành thời gian cho bản thân
-Ngoài những hoạt động trên, em cũng muốn dành một vài giờ mỗi ngày để đọc sách, nghe nhạc, hoặc ngồi ăn những món mà mình thích,..Những khoảnh khắc yên bình này sẽ giúp em thư giãn tâm trí, nhìn lại những điều đã qua và đặt mục tiêu mới cho bản thân trong năm mới
Sáng:
Dọn dẹp nhà cửa, trang trí nhà cửa đón Tết (làm sạch, treo câu đối, trang trí hoa mai, hoa đào, cây cảnh).Chuẩn bị các món ăn truyền thống (bánh chưng, mứt Tết, trà, nước ngọt…).Chiều:
Thăm họ hàng, chúc Tết.Đi siêu thị hoặc chợ để mua sắm thêm đồ Tết.Tối:
Quây quần bên gia đình, cùng nhau làm lễ cúng Giao Thừa.Ăn tối cùng gia đình, trò chuyện, chia sẻ về những kỷ niệm cũ và những dự định trong năm mới.Ngày 2: Thăm bà con, bạn bèSáng:
Dành thời gian thăm ông bà, cha mẹ hoặc người thân lớn tuổi.Chúc Tết và trao đổi những câu chuyện vui vẻ.Chiều:
Thăm bạn bè lâu ngày chưa gặp, trao đổi và ôn lại kỷ niệm.Gửi lời chúc Tết đến bạn bè qua các phương tiện truyền thông xã hội hoặc điện thoại.Tối:
Tham gia các hoạt động vui chơi nhẹ nhàng cùng gia đình hoặc bạn bè (có thể là đi xem pháo hoa, tham gia lễ hội Tết).Ngày 3: Nghỉ ngơi và thư giãnSáng:
Ngủ dậy muộn, thư giãn, thưởng thức một buổi sáng yên tĩnh.Uống trà hoặc cà phê, đọc sách hoặc nghe nhạc thư giãn.Chiều:
Làm các hoạt động yêu thích như tập thể dục, yoga, thiền định hoặc đi dạo ngoài trời.Xem một bộ phim Tết hoặc các chương trình đặc biệt dịp Tết.Tối:
Tạo không gian ấm cúng với ánh đèn, nến, thưởng thức các món ăn nhẹ nhàng như trái cây, bánh mứt.Dành thời gian cho bản thân để tái tạo năng lượng.Ngày 4: Lập kế hoạch cho năm mớiSáng:
Viết nhật ký Tết, ghi lại những điều đã học được trong năm cũ và những mục tiêu cho năm mới.Tạo danh sách các mục tiêu cá nhân, nghề nghiệp, sức khỏe, tài chính.Chiều:
Lập kế hoạch cho việc học tập hoặc công việc trong năm mới, phân bổ thời gian hợp lý.Nghiên cứu thêm về các kỹ năng cần học hoặc các cơ hội nghề nghiệp trong năm tới.Tối:
Xem lại các mục tiêu đã đạt được trong năm cũ và chuẩn bị cho các bước tiếp theo.Ngày 5: Khám phá và du lịch nhẹ nhàngSáng:
Đi tham quan các địa điểm du lịch gần nhà, tham gia vào các lễ hội hoặc các hoạt động văn hóa Tết.Chụp ảnh, ghi lại khoảnh khắc đẹp trong ngày.Chiều:
Nếu có thể, đi xa hơn để khám phá một vùng đất mới, tận hưởng không khí Tết ở nơi khác.Tham gia các trò chơi dân gian hoặc hội chợ xuân.Tối:
Thưởng thức các món đặc sản của vùng miền bạn vừa thăm.Ngày 6: Sáng tạo và phát triển bản thânSáng:
Tham gia vào các hoạt động sáng tạo như vẽ, viết lách, làm đồ thủ công.Hoặc, học thêm một kỹ năng mới mà bạn yêu thích (nấu ăn, vẽ tranh, chơi nhạc cụ).Chiều:
Đọc sách, nghe podcast hoặc tham gia các lớp học trực tuyến.Tiến hành một dự án nhỏ để thử thách khả năng sáng tạo của bản thân.Tối:
Gặp gỡ bạn bè hoặc người thân để chia sẻ những điều bạn đã học được, những cảm hứng mới từ kỳ nghỉ.Ngày 7: Tổng kết và thư giãn cuối tuầnSáng:
Dọn dẹp và sắp xếp lại nhà cửa sau một tuần nghỉ lễ.Lên kế hoạch cho công việc hoặc học tập tuần tới.Chiều:
Dành thời gian thư giãn cuối tuần: xem phim, đọc sách hoặc gặp gỡ bạn bè.Đánh giá lại các mục tiêu đã đề ra và điều chỉnh kế hoạch nếu cần.Tối:
Thưởng thức một bữa tối nhẹ nhàng cùng gia đình, cùng trò chuyện về một tuần đã qua.Tạo không gian thư giãn cuối tuần trước khi trở lại với nhịp sống thường nhật.-Dọn dẹp nhà cửa, trang trí Tết.
-Thăm ông bà, người thân, chúc Tết.
-Đón giao thừa cùng gia đình.
Ngày 2: Nghỉ ngơi-Ngủ nướng, thư giãn.
-Xem phim, đọc sách.
-Dạo phố hoặc đi chơi cùng bạn bè.
Ngày 3: Học hỏi-Học kỹ năng mới (nấu ăn, vẽ…).
-Xem khóa học trực tuyến hoặc đọc sách phát triển bản thân.
Ngày 4: Gia đình-Làm bánh Tết cùng gia đình.
-Chơi trò chơi Tết, thưởng thức bữa cơm gia đình.
Ngày 5: Chăm sóc bản thân-Tập thể dục nhẹ nhàng.
-Thư giãn, đọc sách hoặc làm đẹp.
Ngày 6: Du xuân-Thăm quan địa điểm mới, đi du lịch gần nhà.
-Tham gia lễ hội, hoạt động cộng đồng.
Ngày 7: Tổng kết Tết-Lên kế hoạch cho năm mới.
-Nghỉ ngơi và chuẩn bị cho công việc, học tập.
phân tích đa thức thành nhân tử
a) 2xy + 5x mũ 2y - x3y
b) (x+y) mũ 2 - 9x mũ 2
c 2(x-y)+xy - x mũ 2
d 3x mũ 2 +2x -1
g 5x(x mũ 2- y mũ 2) +2y(x+y)
e -x mũ 2 +4x -3
f x mũ 2-7x+12
a: \(2xy+5x^2y-x^3y\)
\(=xy\cdot2+xy\cdot5x-xy\cdot x^2\)
\(=xy\left(2+5x-x^2\right)\)
b: \(\left(x+y\right)^2-9x^2\)
\(=\left(x+y\right)^2-\left(3x\right)^2\)
\(=\left(x+y+3x\right)\left(x+y-3x\right)=\left(4x+y\right)\left(-2x+y\right)\)
c: \(2\left(x-y\right)+xy-x^2\)
\(=2\left(x-y\right)+x\left(y-x\right)\)
\(=2\left(x-y\right)-x\left(x-y\right)=\left(x-y\right)\left(2-x\right)\)
d: \(3x^2+2x-1\)
\(=3x^2+3x-x-1\)
\(=3x\left(x+1\right)-\left(x+1\right)\)
=(x+1)(3x-1)
g: \(5x\left(x^2-y^2\right)+2y\left(x+y\right)\)
\(=5x\left(x-y\right)\left(x+y\right)+2y\left(x+y\right)\)
\(=\left(x+y\right)\left[5x\left(x-y\right)+2y\right]\)
e: \(-x^2+4x-3\)
\(=-\left(x^2-4x+3\right)\)
\(=-\left(x^2-x-3x+3\right)\)
\(=-\left[x\left(x-1\right)-3\left(x-1\right)\right]\)
\(=-\left(x-1\right)\left(x-3\right)\)
f: \(x^2-7x+12\)
\(=x^2-3x-4x+12\)
=x(x-3)-4(x-3)
=(x-3)(x-4)
Cho ΔABC vuông tại A có AB < AC, đường cao AH. Trên đoạn HC lấy D sao cho HD = HA. Đường vuông góc với BC tại D cắt AC tại E. Gọi M là trung điểm của BE. CM: \(\widehat{AHM}\) = 45\(^o\)
Giúp e với ạ, e cảm ơn nhá ❤
Xét ΔAHD vuông tại H có HA=HD
nên ΔAHD vuông cân tại H
=>\(\widehat{HDA}=\widehat{HAD}=45^0\)
Xét tứ giác EDBA có \(\widehat{EDB}+\widehat{EAB}=90^0+90^0=180^0\)
nên EDBA là tứ giác nội tiếp
=>\(\widehat{AEB}=\widehat{ADB}=45^0\)
Xét ΔAEB vuông tại A có \(\widehat{AEB}=45^0\)
nên ΔAEB vuông cân tại A
=>\(\widehat{ABM}=45^0\)
ΔAEB vuông cân tại A
mà AM là đường trung tuyến
nên AM\(\perp\)BE
Xét tứ giác AMHB có \(\widehat{AMB}=\widehat{AHB}=90^0\)
nên AMHB là tứ giác nội tiếp
=>\(\widehat{AHM}=\widehat{ABM}=45^0\)

Câu 6. (3 điểm) Cho hình vuông \(ABCD\), gọi \(E, F\) thứ tự là trung điểm của \(AB, BC\).
a) Chứng minh rằng: \(CE \perp DF\)
b) Gọi \(M\) là giao điểm của \(CE\) và \(DF\). Chứng minh rằng: \(AM = AD\)
a: Ta có: \(AE=EB=\dfrac{AB}{2}\)
\(BF=FC=\dfrac{BC}{2}\)
mà AB=BC(ABCD là hình vuông)
nên AE=EB=BF=FC
Xét ΔEBC vuông tại B và ΔFCD vuông tại C có
EB=FC
BC=CD
Do đó: ΔEBC=ΔFCD
=>\(\widehat{BEC}=\widehat{CFD}\)
=>\(\widehat{CFD}+\widehat{FCE}=90^0\)
=>CE\(\perp\)DF
b: Gọi K là trung điểm của DC
Ta có: \(AE=EB=\dfrac{AB}{2}\)
\(DK=KC=\dfrac{DC}{2}\)
mà AB=DC(ABCD là hình vuông)
nên AE=EB=DK=KC
Gọi H là giao điểm của AH và DM
Xét tứ giác AECK có
AE//CK
AE=CK
Do đó: AECK là hình bình hành
=>AK//CE
=>AK\(\perp\)DF tại H
Xét ΔDMC có
K là trung điểm của DC
KH//MC
Do đó: H là trung điểm của DM
Xét ΔADM có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔADM cân tại A
=>AM=AD

a) Cho \( a_n = 1 + 2 + 3 + \ldots + n \). Chứng minh rằng \( a_n + a_{n+1} \) là một số chính phương.
Ta có: `a_n=1+2+3+...+n`
`=[(n-1):1+1](n+1)/2=(n(n+1))/2`
`a_(n+1)=1+2+3+...+(n+1)`
`=[(n+1-1):1+1](n+1+1)/2=((n+1)(n+2))/2`
`=>a_n+a_(n+1)`
`=(n(n+1))/2+((n+1)(n+2))/2`
`=(n+1)/2*(n+n+2)`
`=(n+1)(2n+2)/2`
`=(n+1)^2` là số chính phương => Đpcm
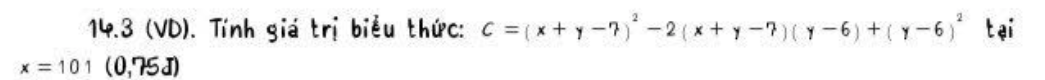
14.3 (VD). Tính giá trị biểu thức: \( C = (x + y - 7)^2 - 2(x + y - 7)(y - 6) + (y - 6)^2 \) tại \( x = 101 \) (0,75đ)
Biểu thức này có dạng khai triển của (a−b)2, trong đó:
a=x+y−7b=y−6
Vậy:
C=[x+y−7−(y−6)]2
Khai triển trong ngoặc:
x+y−7−(y−6)=x−1
Do đó:
C=(x−1)2
Khi x=101, ta có:
C=(101−1)2=1002=10000
Kết luận:
Giá trị của C tại x=101 là 10000
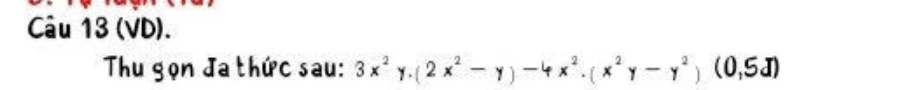
Câu 13 (VD).
Thu gọn đa thức sau: \(3x^2y \cdot (2x^2 - y) - 4x^2 \cdot (x^2y - y^2)\) (0,5đ)
3x²y.(2x² - y) - 4x².(x²y - y²)
= 3x²y.2x² - 3x²y.y - 4x².x²y + 4x².y²
= 6x⁴y - 3x²y² - 4x⁴y + 4x²y²
= (6x⁴y - 4x⁴y) + (-3x²y² + 4x²y²)
= 2x⁴y + x²y²
\(3x^2y\left(2x^2-y\right)-4x^2\left(x^2y-y^2\right)\\ =6x^4y-3x^2y^2-4x^4y+4x^2y^2\\ =\left(-3x^2y^2+4x^2y^2\right)+\left(6x^4y-4x^4y\right)\\ =2x^4y+x^2y^2\)

Bài 1. Tìm giá trị nhỏ nhất của biểu thức \( M = 2x^2 + 4y^2 + 6x - 4y + 2024 \).
Bài 2. Cho \( a^2 + b^2 + c^2 = ab + bc + ca \) và \( a + b + c = 2022 \). Tính \( a, b, c \).
Bài 3. Cho tam giác \( ABC \) vuông ở \( A \). Gọi \( E, G, F \) lần lượt là trung điểm của \( AB, BC, AC \). Từ \( E \) kẻ đường thẳng song song với \( BF \), đường thẳng này cắt \( GF \) tại \( I \).
a) Chứng minh tứ giác \( BEIF \) là hình bình hành.
b) Tìm điều kiện của tam giác \( ABC \) để tứ giác \( AGCI \) là hình vuông.
Bài 1:
\(M=2x^2+4y^2+6x-4y+2024\)
\(=2x^2+6x+\dfrac{9}{2}+4y^2-4y+1+2018,5\)
\(=2\left(x+\dfrac{3}{2}\right)^2+\left(2y-1\right)^2+2018,5>=2018,5\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x+\dfrac{3}{2}=0\\2y-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{3}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\)
Bài 2:
\(a^2+b^2+c^2=ab+bc+ac\)
=>\(2a^2+2b^2+2c^2=2ab+2ac+2bc\)
=>\(\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(a^2-2ac+c^2\right)=0\)
=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\)
=>\(\left\{{}\begin{matrix}a-b=0\\b-c=0\\a-c=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b\\b=c\\a=c\end{matrix}\right.\Leftrightarrow a=b=c\)
Ta có: a=b=c
mà a+b+c=2022
nên \(a=b=c=\dfrac{2022}{3}=674\)
a. xét tứ giác BEIF có:
BF // EI (gt); FI // BE (vì GF là đường trung bình của △ABC)
=> tứ giác BEIF là hình bình hành
b. vì GF là đường trung bình của △ABC
\(\Rightarrow GF=\dfrac{1}{2}AB=EB\left(1\right)\)
mà BE = FI (hình bình hành BEIF) (2)
TỪ (1) (2) => GF = FI
trong △ABC có GB = GC và FA = FC
=> GF là đường trung bình của △ABC
=> GF // AB => \(\widehat{BAC}=\widehat{GFC}=90^0\left(\text{đồng vị}\right)\)
xét tứ giác AGCI có:
FA = FC (gt); FG = FI (cmt)
=> tứ giác AGCI là hình bình hành
lại có \(\widehat{GFC}=90^0\left(cmt\right)\)
=> hình bình hành AGCI là hình thoi
để hình thoi AGCI là hình vuông thì \(\widehat{AGC}=90^0\)
=> AG là đường cao của △ABC; mà AG là đường trung tuyến của △ABC
=> △ABC là △ cân tại A
vậy để tứ giác AGCI là hình vuông thì △ABC là △ vuông cân tại A
SOSSSSSSS.Cần gấp
cho tam giác abc cân tại a.gọi m là trung điểm của bc,n là trung điểm của AC.Trên tia MN lấy điểm D sao cho N là trung điểm của MD
cm:tứ giác ADCM là hình chữ nhật Gọi o là giao điểm của AB và Am.Chứng minh ON là đường trung bình của tam giác BMD và BC=4ON Gọi I là giao điểm của BD Và AC,G là trọng tâm của tam giác ACD,CM IG//BC
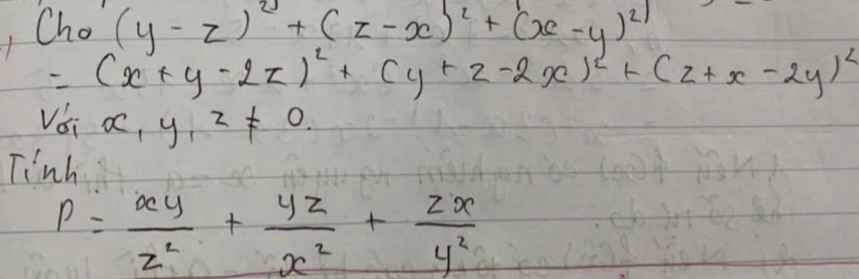 giúp mik vs mik đg cần gấp ạ:(
giúp mik vs mik đg cần gấp ạ:(
Cho \( (y-z)^2 + (z-x)^2 + (x-y)^2 \)
= \( (x+y-2z)^2 + Cy + 2-2x)^2 + Cz + x-2y)^2 \)
Với \( x, y, z \neq 0 \).
Tính:
\[ p = \frac{xy}{z^2} + \frac{yz}{x^2} + \frac{zx}{y^2} \]
Bài 3*: Cho các số x,y thỏa mãn đẳng thức 5x² + 5y² = 8xy + 2x – 2y + 2
Tính giá trị của biểu thức: M=(x + y)^2010 + (x + 2)^2011 + (y - 1)^2012