Câu 7: 

\(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{CB}+\overrightarrow{CA}+\overrightarrow{AD}=\overrightarrow{CB}+\overrightarrow{AD}=-\overrightarrow{DA}+\overrightarrow{CB}\)

=>Loại C

\(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{DB}+\overrightarrow{CB}+\overrightarrow{BD}\)

\(=\overrightarrow{AD}+\overrightarrow{CB}\)

=>Loại B

\(\overrightarrow{AB}-\overrightarrow{DC}=\overrightarrow{AC}+\overrightarrow{CB}-\left(\overrightarrow{DB}+\overrightarrow{BC}\right)\)

\(=\overrightarrow{AC}-\overrightarrow{BC}-\overrightarrow{DB}-\overrightarrow{BC}\)

=>Loại A

=>Chọn D

Câu 8: M thuộc trục Ox nênM(x;0)

A(2;-3); B(3;4); M(x;0)

\(\overrightarrow{AB}=\left(3-2;4+3\right)\)

=>\(\overrightarrow{AB}=\left(1;7\right)\)

\(\overrightarrow{AM}=\left(x-2;3\right)\)

A,M,B thẳng hàng

=>\(\dfrac{x-2}{1}=\dfrac{3}{7}\)

=>\(x=\dfrac{3}{7}+2=\dfrac{17}{7}\)

=>M(17/7;0)

=>Chọn A

Câu 9:

\(\overrightarrow{a}\cdot\overrightarrow{b}=1\cdot\left(-2\right)+\left(-2\right)\cdot\left(-6\right)=12-2=10\)

\(cos\left(\overrightarrow{a};\overrightarrow{b}\right)=\dfrac{10}{\sqrt{1^2+\left(-2\right)^2}\cdot\sqrt{\left(-2\right)^2+\left(-6\right)^2}}=\dfrac{\sqrt{2}}{2}\)

=>\(\left(\overrightarrow{a};\overrightarrow{b}\right)=45^0\)

=>Chọn A

Câu 10: Làm tròn đến độ chính xác d=300 có nghĩa là làm tròn đến hàng nghìn

\(a=15285\simeq15000\)

=>Chọn A

Câu 13:

\(f\left(4\right)=4^2+2\cdot4-1=16+8-1=23\)

f(0)=2-3*0=2

f(4)+f(0)=23+2=25

Câu 1: D

Câu 3: C

Câu 4: A

Câu 5: Xét ΔABC có \(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)

=>\(\dfrac{5^2+8^2-BC^2}{2\cdot5\cdot8}=cos120=-\dfrac{1}{2}\)

=>\(89-BC^2=-40\)

=>\(BC^2=129\)

=>\(BC=\sqrt{129}\)

=>Chọn C

Câu 6: ABCD là hình thoi

=>\(\overrightarrow{AB}=\overrightarrow{DC}\)

=>Vecto DC là vecto cùng hướng với vecto AB

=>Chọn C

M nằm trên trục Ox nên M(x;0)

M(x;0); A(-3;2); B(4;3)

\(\overrightarrow{MA}=\left(-3-x;2\right);\overrightarrow{MB}=\left(4-x;3\right)\)

ΔMAB vuông tại M

=>\(\overrightarrow{MA}\cdot\overrightarrow{MB}=0\)

=>(-3-x)(4-x)+6=0

=>(x-4)(x+3)+6=0

=>\(x^2-x-6=0\)

=>(x-3)(x+2)=0

=>\(\left[{}\begin{matrix}x-3=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)

Vậy: M(3;0); M(-2;0)

a: BM=3CM

=>\(BM=\dfrac{3}{4}BC;CM=\dfrac{1}{4}BC\)

2AN=5MN

=>\(AN=\dfrac{5}{2}MN\)

=>\(AN=\dfrac{5}{7}AM;MN=\dfrac{2}{7}AM\)

\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{BC}\)

\(=\overrightarrow{AB}+\dfrac{3}{4}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{BA}+\dfrac{3}{4}\overrightarrow{AC}\)

\(=\dfrac{1}{4}\cdot\overrightarrow{AB}+\dfrac{3}{4}\cdot\overrightarrow{AC}\)

\(\overrightarrow{BN}=\overrightarrow{BM}+\overrightarrow{MN}\)

\(=\dfrac{3}{4}\overrightarrow{BC}+\dfrac{2}{7}\overrightarrow{MA}\)

\(=\dfrac{3}{4}\overrightarrow{BA}+\dfrac{3}{4}\overrightarrow{AC}+\dfrac{2}{7}\overrightarrow{MB}+\dfrac{2}{7}\overrightarrow{BA}\)

\(=\dfrac{29}{28}\overrightarrow{BA}+\dfrac{3}{4}\overrightarrow{AC}-\dfrac{2}{7}\overrightarrow{BM}\)

\(=-\dfrac{29}{28}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}-\dfrac{2}{7}\cdot\dfrac{3}{4}\cdot\overrightarrow{BC}\)

\(=-\dfrac{29}{28}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}-\dfrac{3}{14}\overrightarrow{BC}\)

\(=-\dfrac{29}{28}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}-\dfrac{3}{14}\overrightarrow{BA}-\dfrac{3}{14}\overrightarrow{AC}\)

\(=-\dfrac{23}{28}\overrightarrow{AB}+\dfrac{15}{28}\overrightarrow{AC}\)

b: G là trọng tâm của ΔABC 

=>\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)

=>\(\overrightarrow{GC}=-\overrightarrow{GA}-\overrightarrow{GB}\)

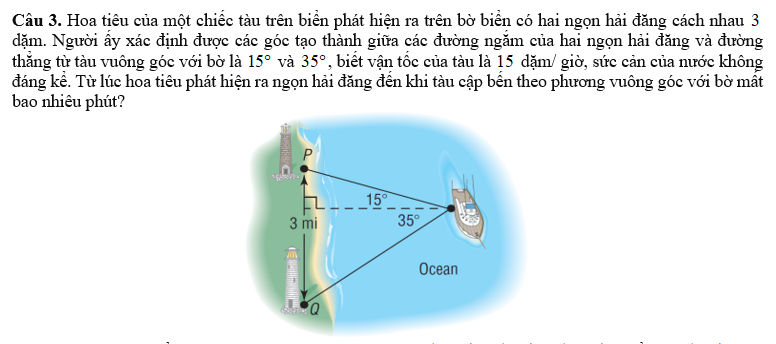
Gọi \(N\) là chân đường cao từ tàu \(T\) đến cạnh \(PQ\)

Xét \(\Delta TNP:tan15^o=\dfrac{PN}{TN}\Rightarrow TN=\dfrac{PN}{tan15^o}\left(1\right)\)

Xét \(\Delta TNQ:tan35^o=\dfrac{QN}{TN}\Rightarrow TN=\dfrac{QN}{tan35^o}\left(2\right)\)

\(\left(1\right);\left(2\right)\Rightarrow\dfrac{PN}{tan15^o}=\dfrac{QN}{tan35^o}\)

mà \(QN=3-PN\left(dặm\right)\)

\(\Rightarrow\dfrac{PN}{tan15^o}=\dfrac{3-PN}{tan35^o}\)

\(\Leftrightarrow PN.tan35^o=3.tan15^o-PN.tan15^o\)

\(\Leftrightarrow PN=\dfrac{3.tan15^o}{tan15^o+tan35^o}\approx0,83\left(dặm\right)\)

\(\left(1\right)\Rightarrow TN=\dfrac{0,83}{tan15^o}\approx3,1\left(dặm\right)\)

Thời gian từ lúc phát hiện hai ngọn hải đăng đến khi tàu cập bến :

\(t=\dfrac{TN}{15}=\dfrac{3,1}{15}\approx0,21\left(giờ\right)=12,6\left(phút\right)\)

Gọi \(x;y>0\) là số tấn Carbon loại 1 và loại 2 sử dụng

Sản xuất ít nhất \(12\) viên kim cương lớn \(5x+2y\ge12\left(1\right)\)

Sản xuất ít nhất \(9\) viên kim cương nhỏ \(3x+3y\ge9\left(2\right)\)

Tổng chi phí mua carbon \(\left(5.20+3.10\right)x+\left(2.20+3.10\right)y\le500\left(triệu.đồng\right)\)

\(\Leftrightarrow130x+70y\le500\left(3\right)\)

Điều kiện về nguyên liệu \(0\le x;y\le4\left(4\right)\)

Từ \(\left(1\right);\left(2\right);\left(3\right);\left(4\right)\) ta có đồ thị

Dựa vào đồ thị ta được \(\left(x;y\right)=\left(2;1\right)\)

\(\left(1\right)\Rightarrow5.2+2.1=12\left(TM\right)\)

\(\left(2\right)\Rightarrow3.2+3.1=9\left(TM\right)\)

Doanh thu bán được là \(130.2+70.1=330\left(triệu.đồng\right)\)