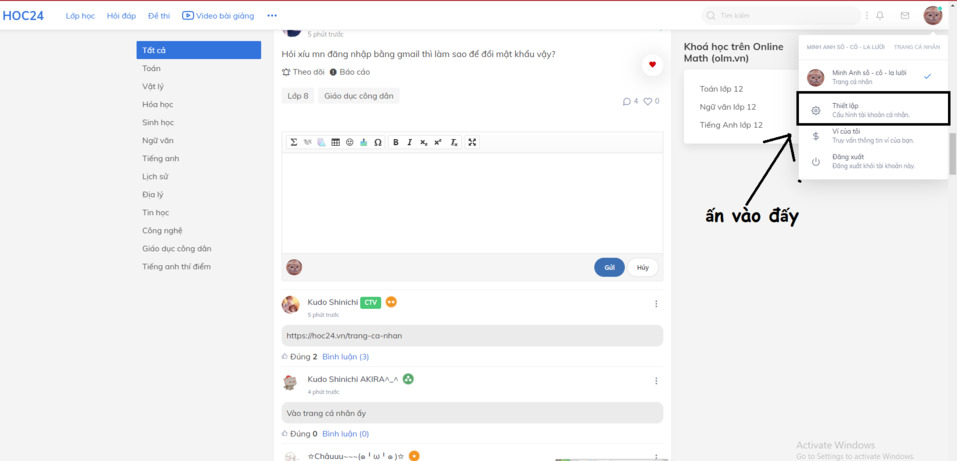
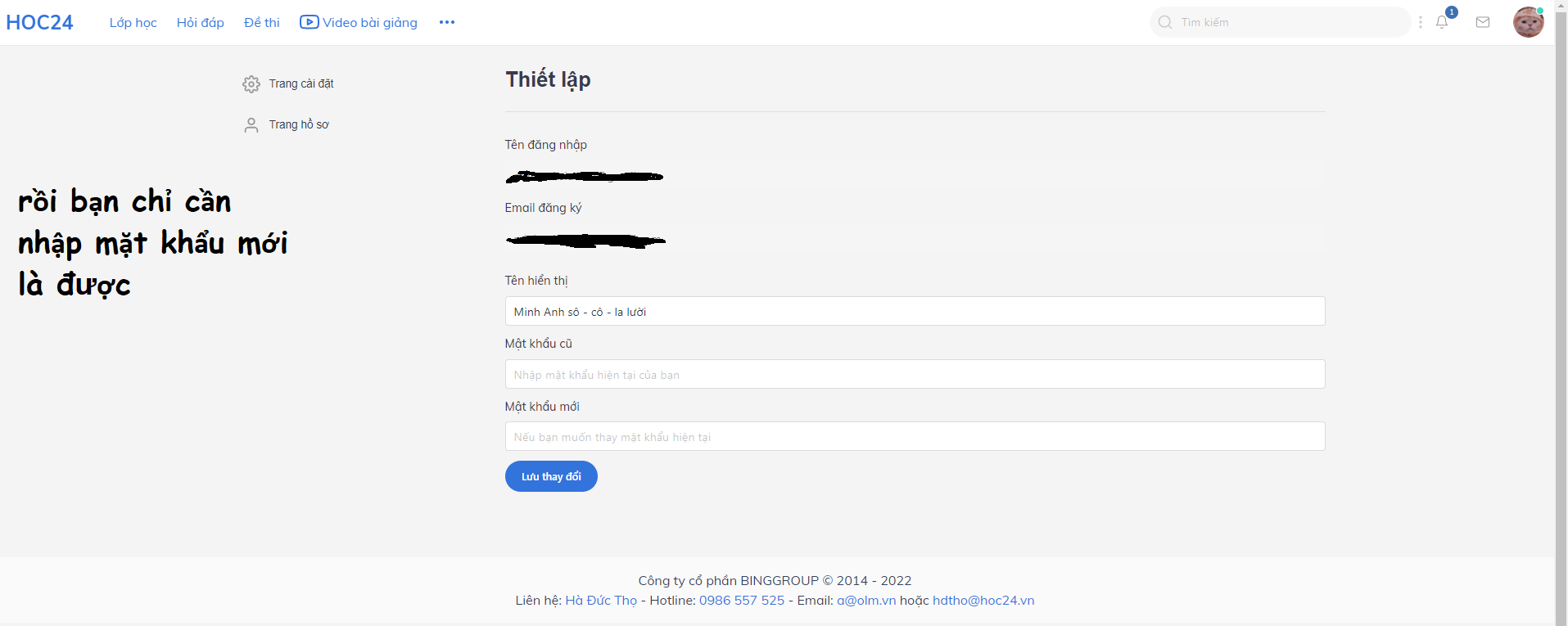
Trước cũng đăng nhập bằng mail rồi ko lấy đc mật khẩu gòi giờ tạo acc mới nè :v
Nếu muốn lấy lại mật khẩu thì chỉ có cách vô phần quên mật khẩu rồi đặt lại nhá :)
`@` Huyy Trần
H2SO4 9,6% `=>` dd loãng
`=>` Khí tạo ra là H2
\(n_{H_2}=\dfrac{1,568}{22,4}=0,07\left(mol\right)\)
`@`TH1: Kết tủa Z thuộc nhóm SO4 . Giả sử BSO4 là kết tủa
\(A+H_2SO_4\rightarrow ASO_4+H_2\) (1)
\(B+H_2SO_4\rightarrow BSO_4\downarrow+H_2\) (2)
\(BSO_4+2AgNO_3\rightarrow B\left(NO_3\right)_2+Ag_2SO_4\downarrow\) (3)
\(n_{Ag_2SO_4}=\dfrac{2,16}{312}=0,007\left(mol\right)\)
\(\left(2\right);\left(3\right)\Rightarrow n_{Ag_2SO_4}=n_B=0,007\left(mol\right)\)
\(\left(1\right);\left(2\right)\Rightarrow n_{H_2\left(p.ứA\right)}=0,07-0,007=0,063\left(mol\right)\)
\(\Rightarrow0,007.M_B+0,063.M_A=5,19\)
\(2M_A+M_B=194\)
`=>` Vô lý ( nghiệm âm )
`@`TH2: Kết tủa Z là kim loại. Giả sử kim loại B là chất ko tan trong dd H2SO4 loãng
\(A+H_2SO_4\rightarrow ASO_4+H_2\) (4)
\(B+2AgNO_3\rightarrow B\left(NO_3\right)_2+2Ag\) (5)
\(n_{Ag}=\dfrac{2,16}{108}=0,02\left(mol\right)\)
\(\left(5\right)\Rightarrow n_B=\dfrac{0,02}{2}=0,01\left(mol\right)\)
\(\left(4\right)\Rightarrow n_A=n_{H_2}=0,07\left(mol\right)\)
\(\Rightarrow m_{hh}=0,07.M_A+0,01.M_B=5,19\)
\(2M_A+M_B=194\)
\(\Rightarrow\left\{{}\begin{matrix}M_A=65\\M_B=64\end{matrix}\right.\) (tm)
Vậy kim loại A là Zn; kim loại B là Cu
dd X là ZnSO4
a.b.\(n_{Al}=\dfrac{5,4}{27}=0,2\left(mol\right)\)
\(n_{HCl}=0,4.2=0,8\left(mol\right)\)
\(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
2 6 2 3 ( mol )
0,2 < 0,8 ( mol )
0,2 0,6 0,2 0,3 ( mol )
\(V_{H_2}=0,3.22,4=6,72\left(l\right)\)
\(C_{M_{AlCl_3}}=\dfrac{0,2}{0,4}=0,5\left(M\right)\)
\(C_{M_{HCl\left(dư\right)}}=\dfrac{0,8-0,6}{0,4}=0,5\left(M\right)\)
c. Nếu cho quỳ tìm vào dd sau phản ứng thì quỳ tím sẽ đổi màu đỏ vì dd HCl còn dư
\(\Delta=3^2-4m\left(m-1\right)\)
\(=9-4m^2+4m\)
\(=-4m^2+4m+9\)
Để ptr có 2 nghiệm \(\Leftrightarrow\Delta\ge0\) (1)
Theo hệ thức Vi-ét, ta có: \(\left\{{}\begin{matrix}S=x_1+x_2=-\dfrac{3}{m}\\P=x_1x_2=\dfrac{m-1}{m}\end{matrix}\right.\)
Để ptr có 2 nghiệm trái dấu \(\Leftrightarrow P< 0\)
\(\Leftrightarrow\dfrac{m-1}{m}< 0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m-1< 0\\m>0\end{matrix}\right.\) hoặc \(\Leftrightarrow\left\{{}\begin{matrix}m-1>0\\m< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 1\\m>0\end{matrix}\right.\)( vô lý ) hoặc \(\Leftrightarrow\left\{{}\begin{matrix}m>1\\m< 0\end{matrix}\right.\) ( vô lý )
Vậy ptr không có 2 nghiệm trái dấu
\(F=\sqrt{2-\sqrt{3}}\left(\sqrt{6}+\sqrt{2}\right)\)
\(\sqrt{2}F=\sqrt{2}\left[\sqrt{2-\sqrt{3}}\left(\sqrt{6}+\sqrt{2}\right)\right]\)
\(\sqrt{2}F=\sqrt{2.\left(2-\sqrt{3}\right)}\left(\sqrt{6}+\sqrt{2}\right)\)
\(\sqrt{2}F=\sqrt{4-2\sqrt{3}}\left(\sqrt{6}+\sqrt{2}\right)\)
\(\sqrt{2}F=\sqrt{\left(\sqrt{3}-1\right)^2}\left(\sqrt{6}+\sqrt{2}\right)\)
\(\sqrt{2}F=\left|\sqrt{3}-1\right|\left(\sqrt{6}+\sqrt{2}\right)\)
\(\sqrt{2}F=\sqrt{2}\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)\) ( cái \(\sqrt{6}+\sqrt{2}\) đặt \(\sqrt{2}\) ra )
\(\sqrt{2}F=\sqrt{2}.2\)
\(F=\dfrac{2\sqrt{2}}{\sqrt{2}}=2\)
Gọi H là giao điểm của EF và AB \(\left(H\in AB\right)\)
Xét \(\Delta CEF\) vuông C có \(IE=IF\) nên \(CI\) là đường trung tuyến của \(\Delta CEF\)
\(\Rightarrow CI=IE=IF\)
\(\Rightarrow\Delta ICE\) cân tại \(I\)
\(\Rightarrow\widehat{ICE}=\widehat{IEC}\)
Mà \(\widehat{IEC}=\widehat{BEH}\) ( đối đỉnh )
\(\Rightarrow\widehat{IEC}=\widehat{BEH}\) (3)
Ta có: \(OC=OB\left(=R\right)\)
\(\Rightarrow\Delta OCB\) cân tại O
\(\Rightarrow\widehat{OCB}=\widehat{OBC}\) (1)
Xét tam giác FAB có AD và BC là 2 đường cao cắt nhau tại E
\(\Rightarrow EF\) là đường cao thứ 3
\(\Rightarrow EH\perp AB\)
Xét tam giác EHB vuông H:
\(\widehat{HEB}+\widehat{HBE}=90^o\) (2)
\(\left(1\right);\left(2\right)\Rightarrow\widehat{OCB}+\widehat{HEB}=90^o\)
\(\left(3\right)\Rightarrow\widehat{OCB}+\widehat{IEC}=90^o\)
\(\Rightarrow\widehat{OCI}=90^o\)
\(\Rightarrow\) IC là tiếp tuyến (O)
\(mx^2-2x+m^2+13=0\)
Để ptr là ptr bậc 2 \(\Leftrightarrow m\ne0\)
\(\Delta=\left(-2\right)^2-4m\left(m^2+13\right)\)
\(=4-4m^3-52m\)
\(=4\left(1-m^3-13m\right)\)
\(=4\left[1-m\left(m^2+13\right)\right]\)
Để ptr có 2 nghiệm trái dấu thì \(\left\{{}\begin{matrix}m\ne0\\4\left[1-m\left(m^2+13\right)\right]>0\\P=\dfrac{m^2+13}{m}< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\1-m\left(m^2+13\right)>0\\\dfrac{m^2+13}{m}< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\1-m\left(m^2+13\right)>0\\m< 0\end{matrix}\right.\) ( vì \(m^2+13>0\left(\forall m\right)\) )