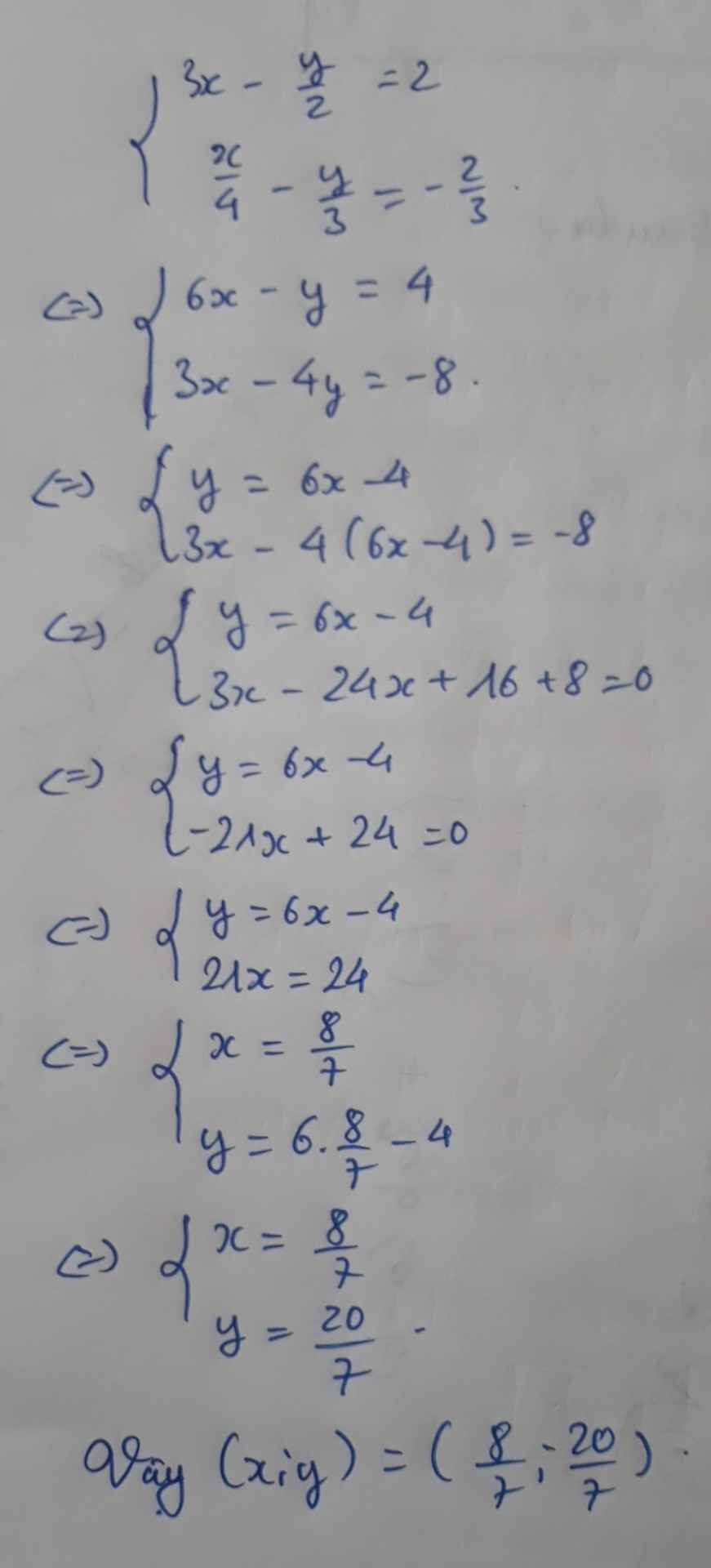`{(3x-y/2 =2 (1)),(x/4 - y/3 = -2/3 (2)):}`
`(1)=>3x = 2 + y/2 <=> x = 2/3 + 1/6 y`
Thay `x=2/3 + 1/6 y` vào `(2)`, ta được:
`(2/3 + 1/6 y)/4 - y/3 = -2/3`
`<=> 1/6 + 1/24 y - y/3 = -2/3`
`<=> 1/6 - 7/24 y = -2/3`
`<=> 7/24 y = 5/6`
`<=> y = 20/7`
Thay `y=20/7` vào `(1)`, ta được:
`3x - (20/7)/2 = 2`
`<=> 3x - 10/7 =2`
`<=>3x=24/7`
`<=>x=8/7`
Vậy `(x;y)=(8/7 ; 20/7)`.
\(\left\{{}\begin{matrix}3x-\dfrac{y}{2}=2\\\dfrac{x}{4}-\dfrac{y}{3}=-\dfrac{2}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x=\dfrac{y}{2}+2\\3x-4y=-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x=\dfrac{y}{2}+2\\\dfrac{y}{2}+2-4y=-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x=\dfrac{y}{2}+2\\\dfrac{7y}{2}=10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}\left(\dfrac{y}{2}+2\right)\\y=\dfrac{20}{7}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}\left(\dfrac{40}{7}+2\right)=\dfrac{1}{3}.\dfrac{54}{7}=\dfrac{18}{7}\\y=\dfrac{20}{7}\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(\dfrac{18}{7};\dfrac{20}{7}\right)\)