Question

Cho hàm số \(f\left(x\right)=\dfrac{2x+m}{x+1}\). Có bao nhiêu giá trị nguyên của tham số m thỏa mãn \(\overset{min\left|f\left(x\right)\right|}{\left[0;2\right]}+\overset{max\left|f\left(x\right)\right|}{\left[0;2\right]}=8\)

Answer 1

\(f\left(x\right)=\dfrac{2x+m}{x+1}\)

\(f'\left(x\right)=\dfrac{2\left(x+1\right)-2x-m}{\left(x+1\right)^2}=\dfrac{2-m}{\left(x+1\right)^2}\)

Xét \(m< 2\Rightarrow f'\left(x\right)>0\forall x\in\left[0,2\right]\)

bbt: 

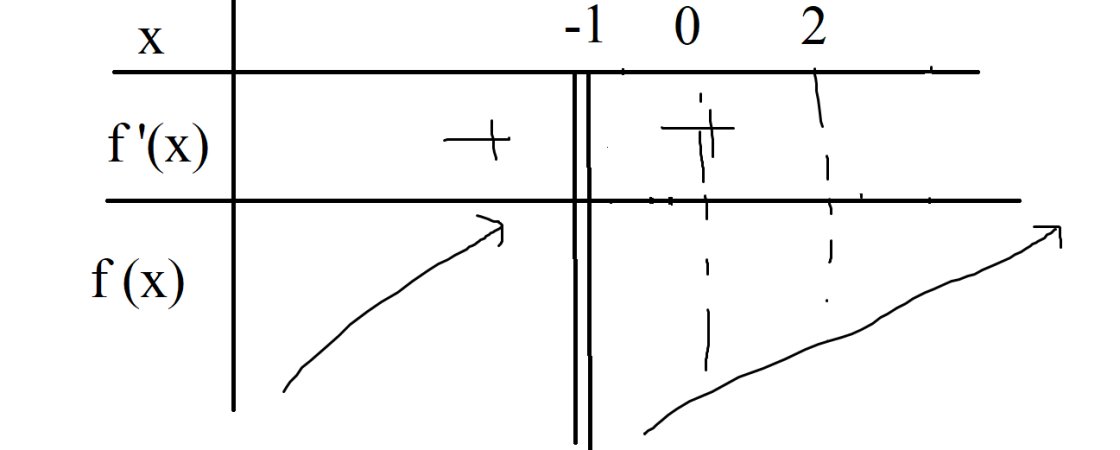
\(\Rightarrow f\left(x\right)_{min\left[0,2\right]}+f\left(x\right)_{max\left[0,2\right]}=f\left(0\right)+f\left(2\right)=m+\dfrac{m+4}{3}=8\Rightarrow m=5\) (thỏa)

Xét \(m>2\Rightarrow f'\left(x\right)< 0\forall x\in\left[0,2\right]\)

bbt:

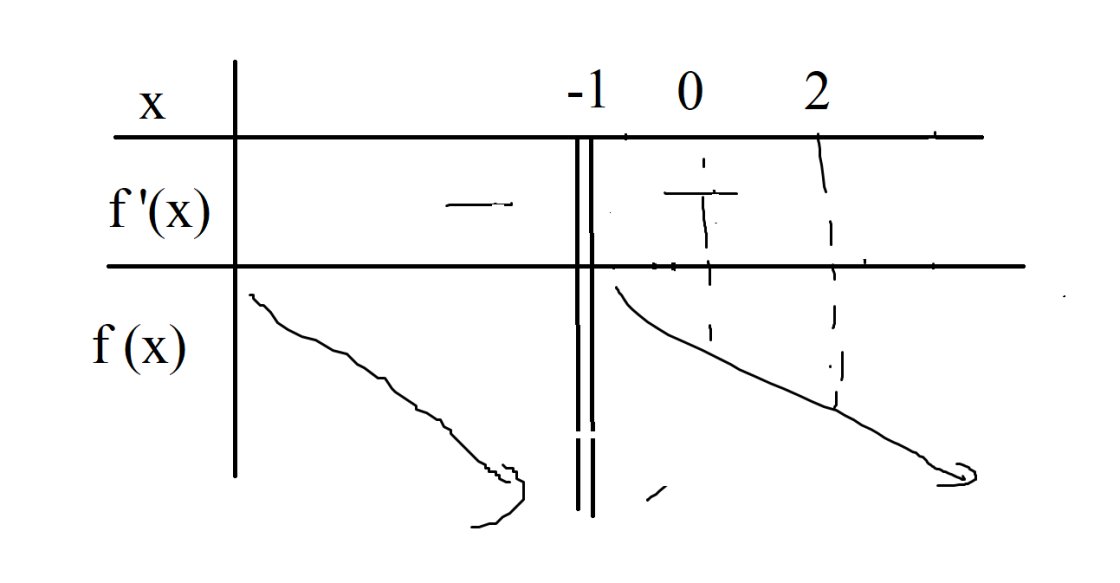
\(\Rightarrow f\left(x\right)_{min\left[0,2\right]}+f\left(x\right)_{max\left[0,2\right]}=f\left(0\right)+f\left(2\right)=m+\dfrac{m+4}{3}=8\Rightarrow m=5\) (loại)

Vậy chỉ có giá trị \(m=5\) thỏa đề