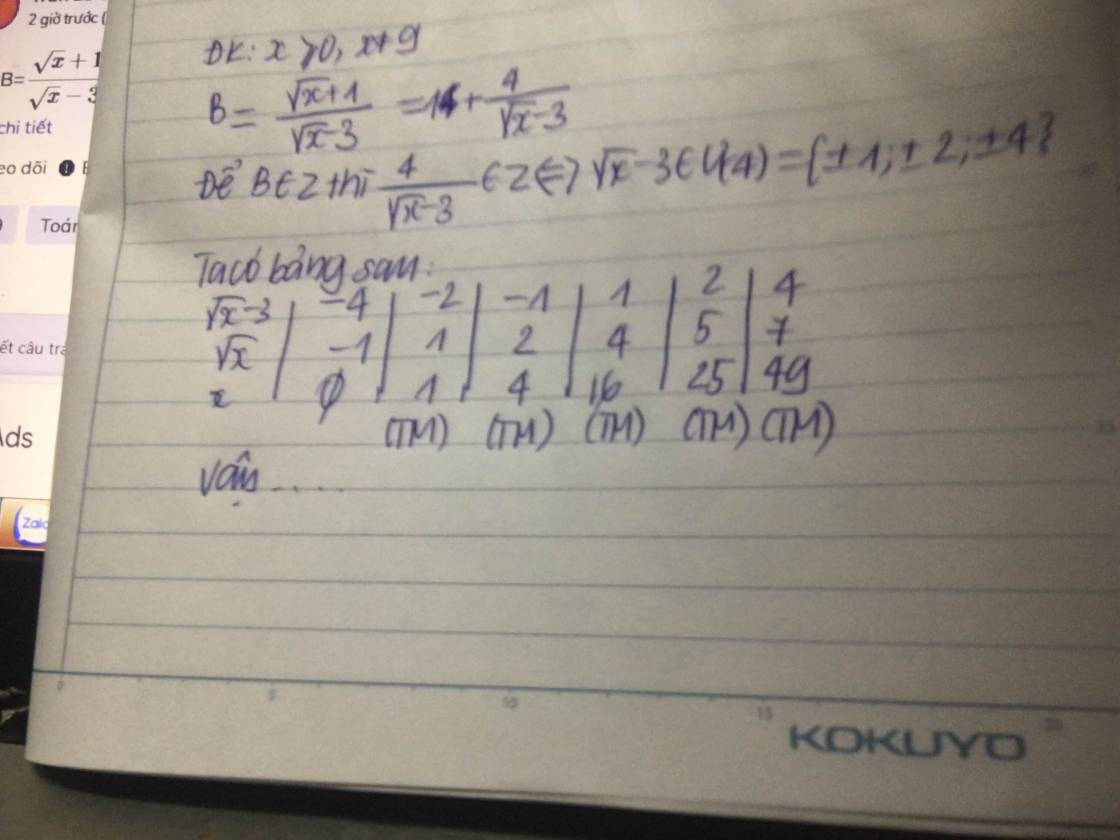Các câu hỏi tương tự
15 tháng 10 2023 lúc 22:23
Adfrac{2sqrt{x}}{sqrt{x}-3} và Bdfrac{2}{sqrt{x}-3}+dfrac{sqrt{x}}{sqrt{x}+3}-dfrac{3-5sqrt{x}}{9-x} với x ≥ 0,x ≠ 9 Tìm các giá trị nguyên của để biểu thức nhận giá trị nguyên.
Đọc tiếp
\(A=\dfrac{2\sqrt{x}}{\sqrt{x}-3}\) và B=\(\dfrac{2}{\sqrt{x}-3}+\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{3-5\sqrt{x}}{9-x}\) với x ≥ 0,x ≠ 9
Tìm các giá trị nguyên của để biểu thức nhận giá trị nguyên.
Cho A= \(\dfrac{\sqrt{x}+4}{{}\sqrt{x}-1}\) và B= \(\dfrac{x+2\sqrt{x}}{\sqrt{x}(\sqrt{x}+1)} -\dfrac{3\sqrt{x}-3}{x-1}\) (đk: x>0,x≠1)
a) Rút gọn P=A.B
b) Tìm x để P(\(\sqrt{x}+1\)) ≤ 6-x
c) Tìm x để P nhận giá trị nguyên
B=\(\left(\dfrac{\sqrt{x}-2}{x-2\sqrt{x}+1}-\dfrac{\sqrt{x}+2}{x-1}\right)\left(x-\sqrt{x}\right)\) Với \(x>0;x\ne1\)
a) Rút gọn biểu thức B
b) Tìm các giá trị nguyên của x để B nhận giá trị nguyên
Tìm x nguyên để \(\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\) nhận giá trị nguyên
A=\(\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\) và B=\(\dfrac{-3\sqrt{x}-3}{x-9}\) Tìm giá trị x nguyên để P=B:A đạt giá trị nguyên
Tìm x nguyên để P=\(\dfrac{\sqrt{x}+5}{3\sqrt{x}+1}\) nhận giá trị nguyên
Tìm giá trị nguyên của x để biểu thức \(P=\dfrac{B}{A}\) có giá trị nguyên biết A =\(\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\) và B =\(\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\)
Cho biểu thức \(Q=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2x-2}{\sqrt{x}-1}\)
a, Rút gọn rồi tìm giá trị nhỏ nhất của Q
b, Tìm các số nguyên x để \(\dfrac{3Q}{\sqrt{x}}\) nhận giá trị nguyên
6 tháng 8 2023 lúc 20:56
Bài 3: Cho biểu thức: \(A=\dfrac{2x-3\sqrt{x}-2}{\sqrt{x}-2},\) với \(x\ge0\) và x \(\ne4\)
a) Rút gọn A rồi tìm giá trị của x để A \(\le5\)
b) Tìm các giá trị của x để \(\dfrac{A}{2}\) nhận giá trị nguyên