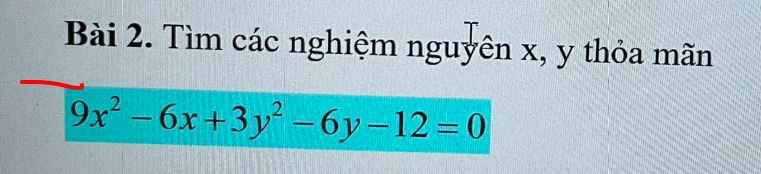`9x^2-6x+3y^2-6y-12=0`
`<=>(9x^2-6x+1)+(3y^2-6y+3)-16=0`
`<=>(3x-1)^2+3(y-1)^2=16`
Đặt `3x-1=a;y-1=b`
`pt<=>a^2+3b^2=14`
`<=>a^2=16-3b^2`
Nhận thấy nếu `(a_0;b_0)` là nghiệm thì `(a_0;-b_0)` cũng là nghiệm, nên ta xét `b>=0`
- Nếu `b=0=>a^2=16=>a=+-4`
- Nếu `b=1=>a^2=13=>` Loại do `pt` không có nghiệm nguyên.
- Nếu `b=2=>a^2=4=>a=+-2`
- Nếu `b>=3` thì `a^2=16-3b^2<=16-3.3^2=-11(` Vô lý do `a^2>=0AAa)`
Khi đó ta có: `(a;b)\in{(+-4;0),(+-2;+-2)}`
`=>(3x-1;y-1)\in{(+-4;0),(+-2;+-2)}`
mà `3x-1` chia `3` dư `-1` nên `(3x-1;y-1)\in{(-4;0),(2;+-2)}`
`=>(x;y)\in{(-1;1),(1;3),(1;-1)}`
Vậy `(x;y)\in{(-1;1),(1;3),(1;-1)}`