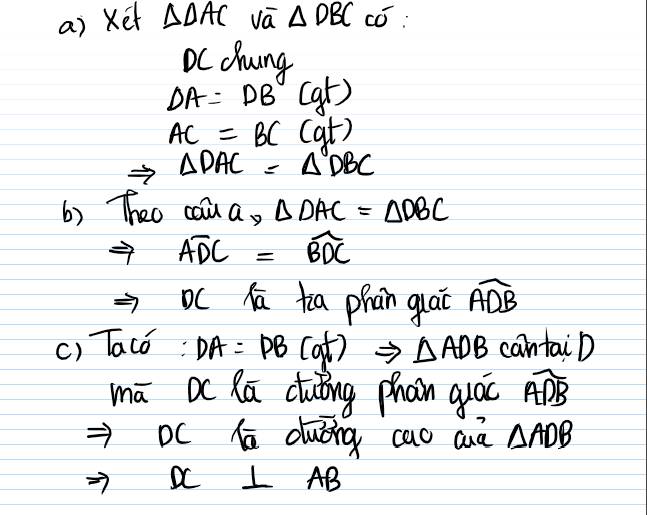a)Xét \(\Delta DAC\) và \(\Delta DBC\) có:
\(DA=DB\left(gt\right)\)
\(DC\) chung
\(CA=CB\left(gt\right)\)
\(\Rightarrow\Delta DAC=\Delta DBC\left(c.c.c\right)\)
b)Do \(\Delta DAC=\Delta DBC\left(chungminhcaua\right)\)
\(\Rightarrow\widehat{ADC}=\widehat{BDC}\)
Do đó DC là tia phân giác của \(\widehat{ADB}\)
c)Do \(CA=CB\left(gt\right)\)
\(\Rightarrow C\) thuộc đường trung trực của \(AB\)
Do đó \(DC\) là đường trung trực của \(AB\) hay \(DC\perp AB\)
a) Tam giác `DAC` và Tam giác `DBC` có:
`Ad = DB (gt)`
`DC` chung
`AC = CB (gt)`
=> Tam giác `DAC =` Tam giác `DBC` (cạnh - cạnh - cạnh)
b) Theo a, ta có: Tam giác ` DAC =` Tam giác `DBC`
`=> hat{ADC} = hat{CDB}`
`=> DC` là tia phân giác của `hat{ADB}`
c) Kéo dài `DC` cắt `AB` tại `H
Tam giác `ADH` và Tam giác `BDH` có:
`AD = DB (gt)`
`hat{ADC} = hat{CDB} (cmt)`
`DH` chung
`=>` Tam giác `ADH` và Tam giác `BDH` (cạnh - góc -cạnh)
`=> hat{DHA} = hat{DHB} = 1/2 hat{AHB}`
`=> hat{DHA} = 1/2 . 180^o`
`=> hat{DHA} = 90^o`
`=> DH ⊥ AD hay DC ⊥ AB (đpcm)`
a: Xét ΔDAC và ΔDBC có
DA=DB
AC=BC
DC chung
=>ΔDAC=ΔDBC
b: ΔDAC=ΔDBC
=>góc ADC=góc BDC
=>DC là phân giác của góc ADB
c: ΔDAB cân tại D
mà DC làphân giác
nên DC vuông góc AB
a.Xét ΔDAC và ΔDBC có ;
AD=DB<gt>
AC=BC<gt>
DC chung
⇒ΔDAC=ΔDBC<c-c-c>
Phần b,c mik quên cách làm r ,thông cảm nha !
`a)`
Xét `Delta ADC` và `Delta DBC` có :
`{:(DA=DB(GT)),(DC-chung),(AC=BC(GT)):}}`
`=>Delta ADC=Delta DBC(c.c.c)(đpcm)`
`b)`
Có `Delta ADC=Delta DBC(cmt)=>hat(ADC)=hat(CDB)` ( 2 góc t/ứng)
mà `DC` nằm giữa `DA` và `DB`
nên `DC` là p/g của `hat(ADB)(đpcm)`
`c)`
Có `AD=DB(GT)=>D in ` trung trực của `AB` (1)
`CA=CB(GT)=>C in ` trung trực của `AB` (2)
Từ (1) và (2) suy ra `DC` là trung trực của`AB`
`=>DC⊥AB`