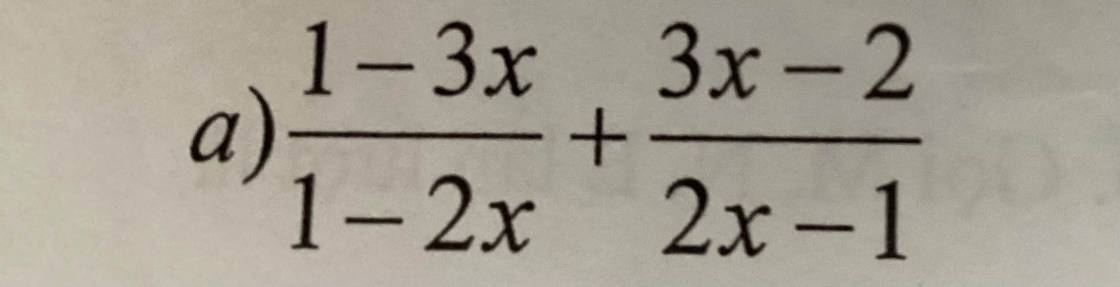Question

Answer 1

`[1-3x]/[1-2x]+[3x-2]/[2x-1]`     `ĐK: x \ne 1/2`

`=[1-3x+2-3x]/[1-2x]`

`=[3-6x]/[1-2x]`

`=[3(1-2x)]/[1-2x]=3`

Answer 2

\(\dfrac{1-3x}{1-2x}+\dfrac{3x-2}{2x-1}\\ =\dfrac{1-3x}{1-2x}-\dfrac{3x-2}{1-2x}\\ =\dfrac{1-3x-3x+2}{1-2x}\\ =\dfrac{3-6x}{1-2x}\\ =\dfrac{3\left(1-2x\right)}{1-2x}\\ =3\)

Answer 3

\(=\dfrac{3x-1+3x-2}{2x-1}=\dfrac{6x-3}{2x-1}=3\)

Answer 4

`(1-3x)/(1-2x) + (3x-2)/(2x-1)`

`= (1-3x)/(1-2x) - (3x-2)/(1-2x)`

`= (1-3x -(3x-2))/(1-2x)`

`=  (1-3x -3x+2)/(1-2x)`

`= (3-6x)/(1-2x)`

`=(3(1-2x))/((1-2x)`

`=3`

Answer 5

1-3x/1-2x+3x-2/2x-1

=1-3x/1-2x-3x+2/1-2x

=1-3x-3x+2/1-2x

=3-6x/1-2x

=3(1-2x)/1-2x

=3