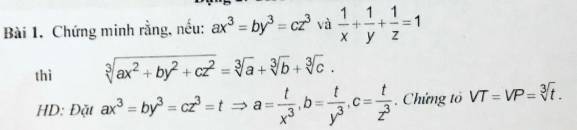Question

Answer 1

Đặt \(ax^3=by^3=cz^3=t\Rightarrow a=\dfrac{t}{x^3},b=\dfrac{t}{y^3},c=\dfrac{t}{z^3}.\) Khi đó, ta có:

\(VT=\sqrt[3]{ax^2+by^2+cz^2}=\sqrt[3]{x^2.\dfrac{t}{x^3}+y^2.\dfrac{t}{y^3}+z^2.\dfrac{t}{z^3}}=\sqrt[3]{\dfrac{t}{x}+\dfrac{t}{y}+\dfrac{t}{z}}=\sqrt[3]{t\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)}=\sqrt[3]{t}\)

\(VP=\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}=\sqrt[3]{\dfrac{t}{x^3}}+\sqrt[3]{\dfrac{t}{y^3}}+\sqrt[3]{\dfrac{t}{z^3}}=\dfrac{\sqrt[3]{t}}{x}+\dfrac{\sqrt[3]{t}}{y}+\dfrac{\sqrt[3]{t}}{z}=\sqrt[3]{t}\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)=\sqrt[3]{t}\)

Từ đó, suy ra: \(VT=VP\)

Ta có: đpcm