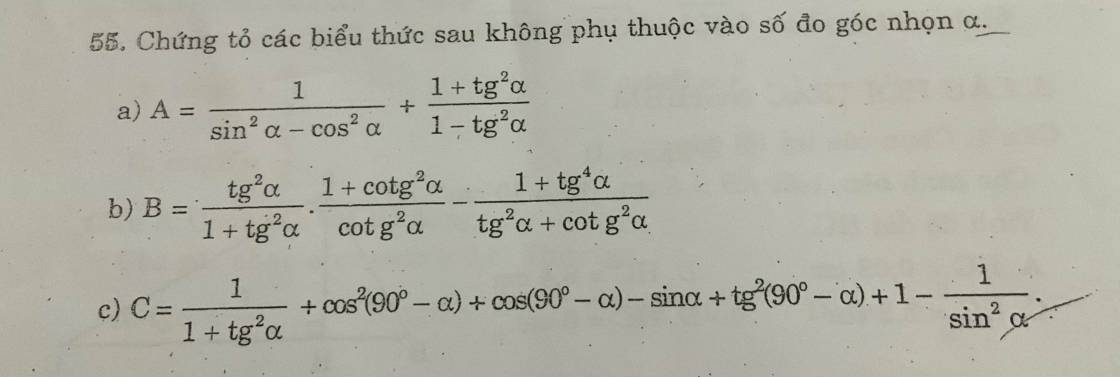a) \(A=\dfrac{1}{sin^2\alpha-cos^2\alpha}+\dfrac{1+tg^2\alpha}{1-tg^2\alpha}\)
\(=\dfrac{1}{tg^2\alpha.cos^2\alpha-cos^2\alpha}-\dfrac{tg^2\alpha+1}{tg^2\alpha-1}\)
\(=\dfrac{1}{cos^2\alpha\left(tg^2\alpha-1\right)}-\dfrac{tg^2\alpha+1}{tg^2\alpha-1}\)
\(=\dfrac{1-cos^2\alpha\left(tg^2\alpha+1\right)}{cos^2\alpha\left(tg^2\alpha-1\right)}\)
\(=\dfrac{1-cos^2\alpha.tg^2\alpha-cos^2\alpha}{cos^2\alpha\left(tg^2\alpha-1\right)}\)
\(=\dfrac{1-sin^2\alpha-cos^2\alpha}{cos^2\alpha\left(tg^2\alpha-1\right)}\)
\(=\dfrac{1-1}{cos^2\alpha\left(tg^2\alpha-1\right)}\)
\(=\dfrac{0}{cos^2\alpha\left(tg^2\alpha-1\right)}\)
\(=0\)
b) \(B=\dfrac{tg^2\alpha}{1+tg^2\alpha}.\dfrac{1+cotg^2\alpha}{cotg^2\alpha}-\dfrac{1+tg^4\alpha}{tg^2\alpha+cotg^2\alpha}\)
\(=\dfrac{tg^2\alpha\left(1+cotg^2\alpha\right)}{cotg^2\alpha\left(1+tg^2\alpha\right)}-\dfrac{tg^2\alpha.cotg^2\alpha+tg^4\alpha}{tg^2\alpha+cotg^2\alpha}\)
\(=\dfrac{tg^2\alpha+tg^2\alpha.cotg^2\alpha}{cotg^2\alpha+tg^2\alpha.cotg^2\alpha}-\dfrac{tg^2\alpha\left(tg^2\alpha+cotg^2\alpha\right)}{tg^2\alpha+cotg^2\alpha}\)
\(=\dfrac{tg^2\alpha+1}{cotg^2\alpha+1}-tg^2\alpha\)
\(=\dfrac{tg^2\alpha+1-tg^2\alpha\left(cotg^2\alpha+1\right)}{cotg^2\alpha+1}\)
\(=\dfrac{tg^2\alpha+1-tg^2\alpha.cotg^2\alpha-tg^2\alpha}{cotg^2\alpha+1}\)
\(=\dfrac{1-1}{cotg^2\alpha+1}\)
\(=\dfrac{0}{cotg^2\alpha+1}\)
\(=0\)
c) \(C=\dfrac{1}{1+tg^2\alpha}+cos^2\left(90^0-\alpha\right)+cos\left(90^0-\alpha\right)-sin\alpha+tg^2\left(90^0-\alpha\right)+1-\dfrac{1}{sin^2\alpha}\)
\(=\dfrac{1}{1+tg^2\alpha}+sin^2\alpha+sin\alpha-sin\alpha+cotg^2\alpha+1-\dfrac{sin^2\alpha+cos^2\alpha}{sin^2\alpha}\)
\(=\dfrac{1}{1+tg^2\alpha}+sin^2\alpha+cotg^2\alpha+1-1-\dfrac{cos^2\alpha}{sin^2\alpha}\)
\(=\dfrac{1}{1+tg^2\alpha}+sin^2\alpha+cotg^2\alpha-cotg^2\alpha\)
\(=\dfrac{1}{1+tg^2\alpha}+sin^2\alpha\)
\(=\dfrac{1}{1+\dfrac{sin^2\alpha}{cos^2\alpha}}+sin^2\alpha\)
\(=\dfrac{1}{\dfrac{sin^2\alpha+cos^2\alpha}{cos^2\alpha}}+sin^2\alpha\)
\(=\dfrac{1}{\dfrac{1}{cos^2\alpha}}+sin^2\alpha\)
\(=cos^2\alpha+sin^2\alpha\)
\(=1\)