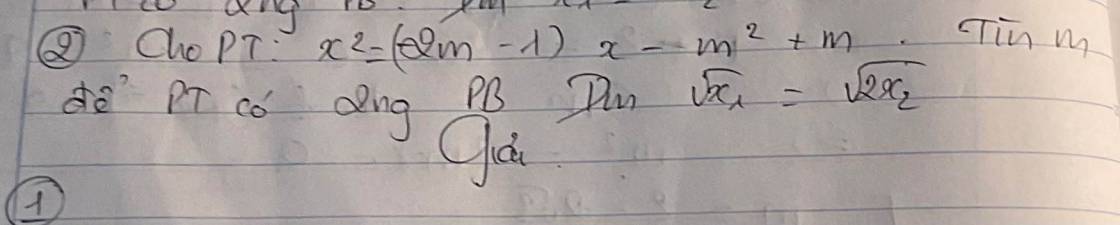Pt <=> x2 - (2m - 1)x + m2 - m = 0
Đk pt có 2 nghiệm pb là:
\(\Delta=\left(2m-1\right)^2-4\left(m^2-m\right)>0\)
\(\Leftrightarrow4m^2-4m+1-4m^2+4m>0\)
<=> 1 > 0 (luôn đúng)
Theo hệ thức Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m-1\\x_1x_2=m^2-m\end{matrix}\right.\)
Mặt khác, vì pt có 2 nghiệm pb tm \(\sqrt{x_1}=\sqrt{2x_2}\) nên điều kiện xác định là:
\(\left\{{}\begin{matrix}x_1\ge0\\2x_2\ge0\end{matrix}\right.\Leftrightarrow2x_1x_2\ge0\Leftrightarrow m^2-m\ge0\Leftrightarrow m\ge1\)
Ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m-1\\\sqrt{x_1}=\sqrt{2x_2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=2x_2\\3x_2=2m-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{4m-2}{3}\\x_2=\dfrac{2m-1}{3}\end{matrix}\right.\)
Ta có: \(x_1x_2=m^2-m\)
\(\Leftrightarrow\dfrac{4m-2}{3}.\dfrac{2m-1}{3}=m^2-m\)
\(\Leftrightarrow\dfrac{2\left(2m-1\right)^2}{9}=m^2-m\)
\(\Leftrightarrow8m^2-8m+2=9m^2-9m\)
\(\Leftrightarrow m^2-m-2=0\)
Ta có: a - b + c = 1 + 1 - 2 = 0 nên phương trình có 2 nghiệm pb là: \(\left[{}\begin{matrix}m=-1\\m=2\end{matrix}\right.\)
So với điều kiện xác định thấy m = 2 thỏa mãn
Vậy với m = 2 thì pt có 2 nghiệm pb tm \(\sqrt{x_1}=\sqrt{2x_2}\)