\(a)\)\(\dfrac{2-\sqrt{2}}{\sqrt{2}}=\dfrac{\sqrt{2}\left(\sqrt{2}-1\right)}{\sqrt{2}}=\sqrt{2}-1\)
\(b)\)\(\dfrac{\sqrt{2}+\sqrt{3}}{2+\sqrt{6}}=\dfrac{\sqrt{2}+\sqrt{3}}{\sqrt{2}\left(\sqrt{2}+\sqrt{3}\right)}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
\(c)\)\(\dfrac{a+\sqrt{a}}{\sqrt{a}}=\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}}=\sqrt{a}+1\left(ĐK:a>0\right)\)
\(d)\)\(\dfrac{3+\sqrt{3}}{1+\sqrt{3}}=\dfrac{\sqrt{3}\left(\sqrt{3}+1\right)}{\sqrt{3}+1}=\sqrt{3}\)
\(e)\)\(\dfrac{\sqrt{a}-a}{\sqrt{a}-1}=\dfrac{-\sqrt{a}\left(-1+\sqrt{a}\right)}{-1+\sqrt{a}}=-\sqrt{a}\left(ĐK:a>=0;a\ne1\right)\)
\(g)\)\(\dfrac{a-b}{\sqrt{a}-\sqrt{b}}=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}=\sqrt{a}+\sqrt{b}\left(ĐK:a,b>=0;a\ne b\right)\)
\(i)\)\(\dfrac{x\sqrt{x}-y\sqrt{y}+x\sqrt{y}-y\sqrt{x}}{x+y+2\sqrt{xy}}\\ =\dfrac{x\left(\sqrt{x}+\sqrt{y}\right)-y\left(\sqrt{x}+\sqrt{y}\right)}{\left(\sqrt{x}+\sqrt{y}\right)^2}\\ =\dfrac{\left(\sqrt{x}+\sqrt{y}\right)\left(x-y\right)}{\left(\sqrt{x}+\sqrt{y}\right)^2}\\ =\dfrac{x-y}{\sqrt{x}+\sqrt{y}}\\ =\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}+\sqrt{y}}=\sqrt{x}-\sqrt{y}\left(ĐK:x,y>=0;\sqrt{x}+\sqrt{y}\ne0\right)\)\(\dfrac{a+b+2\sqrt{ab}}{\sqrt{a}+\sqrt{b}}=\dfrac{\left(\sqrt{a}+\sqrt{b}\right)^2}{\sqrt{a}+\sqrt{b}}=\sqrt{a}+\sqrt{b}\left(ĐK:a,b>=0;\sqrt{a}+\sqrt{b}\ne0\right)\)
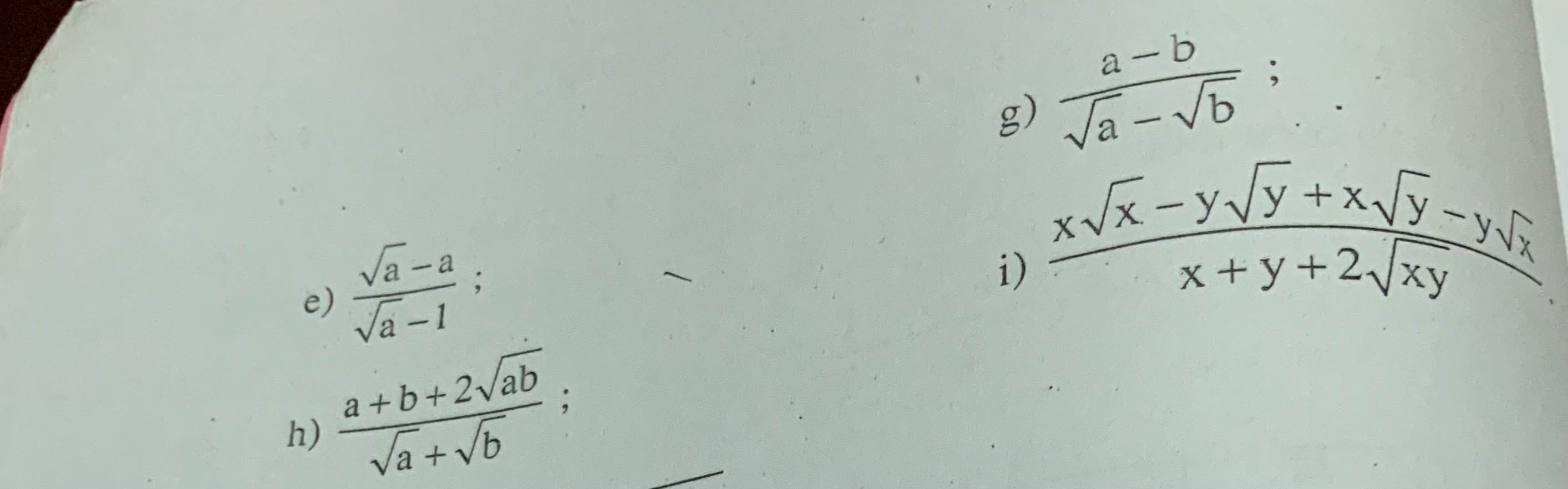
có gì không hiểu thì hỏi mk nhé
