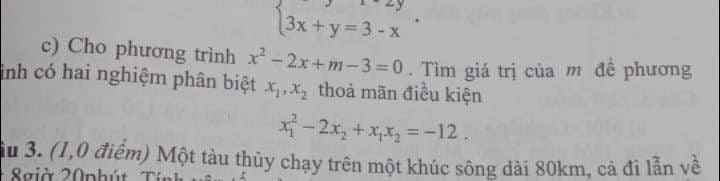Question

Answer 1

\(\Delta'=4-m\)

để phương trình có 2 nghiệm phân biệt => m <4 

với m <4 theo viet :

\(\left\{{}\begin{matrix}x1+x2=2\left(1\right)\\x1.x2=m-3\left(3\right)\end{matrix}\right.\)

vì x1 là nghiệm của phương trình \(x^2-2x+m-3=0\)

thay x=x1 vào phương trình ta được \(x1^2=2x1-m+3\)

thay \(x1^2=2x1-m+3\) vào phương trình \(x1^2-2x2+x1x2=-12\)

<=> \(2x1-m+3-2x2+m-3=-12< =>2x1-2x2=-12\left(2\right)\)

từ 1 và 2 ta có hpt 

\(\left\{{}\begin{matrix}x1+x2=2\\2x1-2x2=-12\end{matrix}\right.< =>\left\{{}\begin{matrix}x1=-2\\x2=4\end{matrix}\right.\)

thay x1=-2 x2=4 vào phương trình 3 ta được 

-2.4=m-3<=>m=-5 (tm)