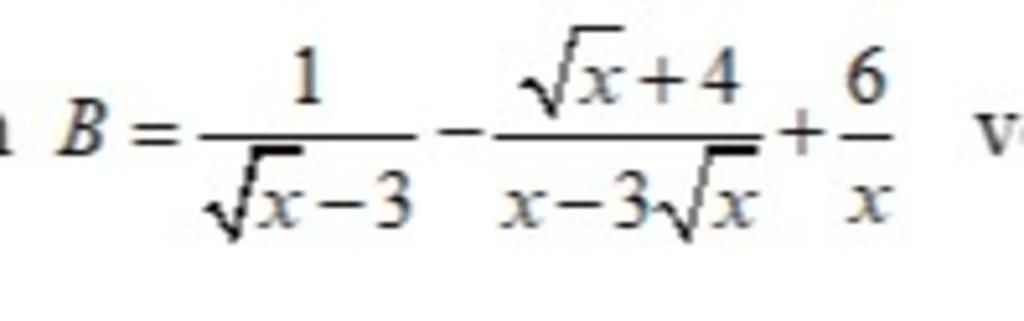Nhận thấy \(\dfrac{x-3\sqrt{x}}{\sqrt{x}-3}=\dfrac{\left(\sqrt{x}-3\right)\sqrt{x}}{\sqrt{x}-3}=\sqrt{x}\), thì ta có:
+)ĐKXĐ của biểu thức B là: \(\left[{}\begin{matrix}x>0\\\sqrt{x}-3\ne0\Leftrightarrow\sqrt{x}\ne3\Leftrightarrow x\ne9\end{matrix}\right.\)
\(B=\dfrac{1}{\sqrt{x}-3}-\dfrac{\sqrt{x}+4}{x-3\sqrt{x}}+\dfrac{6}{x}\) với \(x>0\); \(x\ne9\)
\(=\dfrac{\sqrt{x}}{\left(\sqrt{x}-3\right)\sqrt{x}}-\dfrac{\sqrt{x}+4}{x-3\sqrt{x}}+\dfrac{6}{x}\\ =\dfrac{\sqrt{x}-\sqrt{x}-4}{\left(\sqrt{x}-3\right)\sqrt{x}}+\dfrac{6}{\sqrt{x}^2}\\=\dfrac{\left(\sqrt{x}-3\right)\cdot6}{\left(\sqrt{x}-3\right)\sqrt{x}^2}-\dfrac{4\sqrt{x}}{\left(\sqrt{x}-3\right)\sqrt{x}^2} \)
\(=\dfrac{6\sqrt{x}-18-4\sqrt{x}}{\left(\sqrt{x}-3\right)x}\\=\dfrac{2\sqrt{x}-18}{x\sqrt{x}-3x} \)