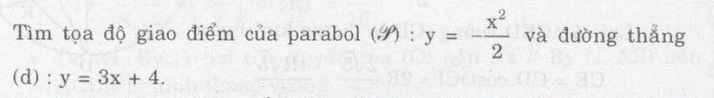Question

Answer 1

+)Ta có hệ phương trình sau: \(\left\{{}\begin{matrix}y=3x+4\\y=-\dfrac{x^2}{2}\end{matrix}\right.\)

Từ hệ phương trình trên, ta được: \(3x+4=\dfrac{-\left(x^2\right)}{2}\\\Leftrightarrow\left(3x+4\right)\cdot2=-\left(x^2\right)\\\Leftrightarrow6x+8=-\left(x^2\right)\\\Leftrightarrow x^2+4x+2x+8=0\\\Leftrightarrow\left(x+4\right)\left(x+2\right)=0 \)

                                                       \(\Leftrightarrow\left[{}\begin{matrix}x+4=0\Leftrightarrow x=-4\\x+2=0\Leftrightarrow x=-2\end{matrix}\right.\)

+)Với \(x=-2\) ⇔ \(y=-\dfrac{x^2}{2}=-\dfrac{\left(-2\right)^2}{2}=-\dfrac{4}{2}=-2\)

+) Với \(x=-4\) ⇔ \(y=-\dfrac{x^2}{2}=-\dfrac{\left(-4\right)^2}{2}=-\dfrac{16}{2}=-8\)

➤Tọa độ giao điểm của parabol là: \(\left(x;y\right)=\left(-2;-2\right)\) hoặc \(\left(x;y\right)=\left(-4;-8\right)\)