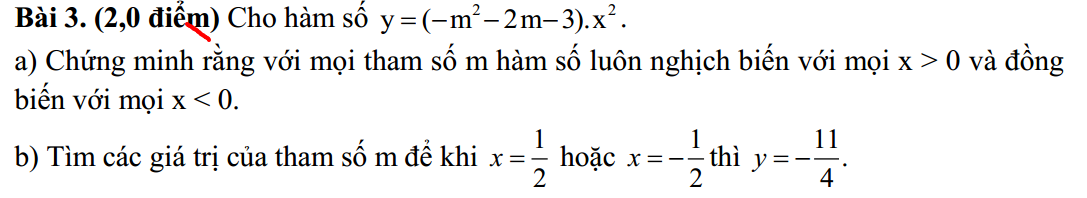a, để hs trên luôn nghịch biến với x > 0
\(\Leftrightarrow-m^2-2m-3< 0\Leftrightarrow-\left(m^2+2m+3\right)< 0\)
\(\Leftrightarrow-\left(m^2+2m+1+2\right)< 0\Leftrightarrow-\left(m+1\right)^2-2< 0\)
* luôn đúng *
b, để hs trên luôn đồng biến với mọi x < 0
\(\Leftrightarrow-m^2-2m-3>0\Leftrightarrow-\left(m+1\right)^2-2>0\)( vô lí )
b, Thay x = 1/2 ; y = -11/4 vào hs trên ta được
\(\dfrac{-m^2-2m-3}{4}=-\dfrac{11}{4}\Rightarrow-m^2-2m+8=0\)
\(\Leftrightarrow m^2+2m-8=0\Leftrightarrow\left(m+1\right)^2-9=0\Leftrightarrow\left(m-2\right)\left(m+4\right)=0\Leftrightarrow m=-4;m=2\)
Thay x = -1/2 ; y = 11/4 vào hs trên ta được
\(\dfrac{\left(-m^2-2m-3\right)\left(-1\right)^2}{4}=-\dfrac{11}{4}\Rightarrow m=-4;m=2\)