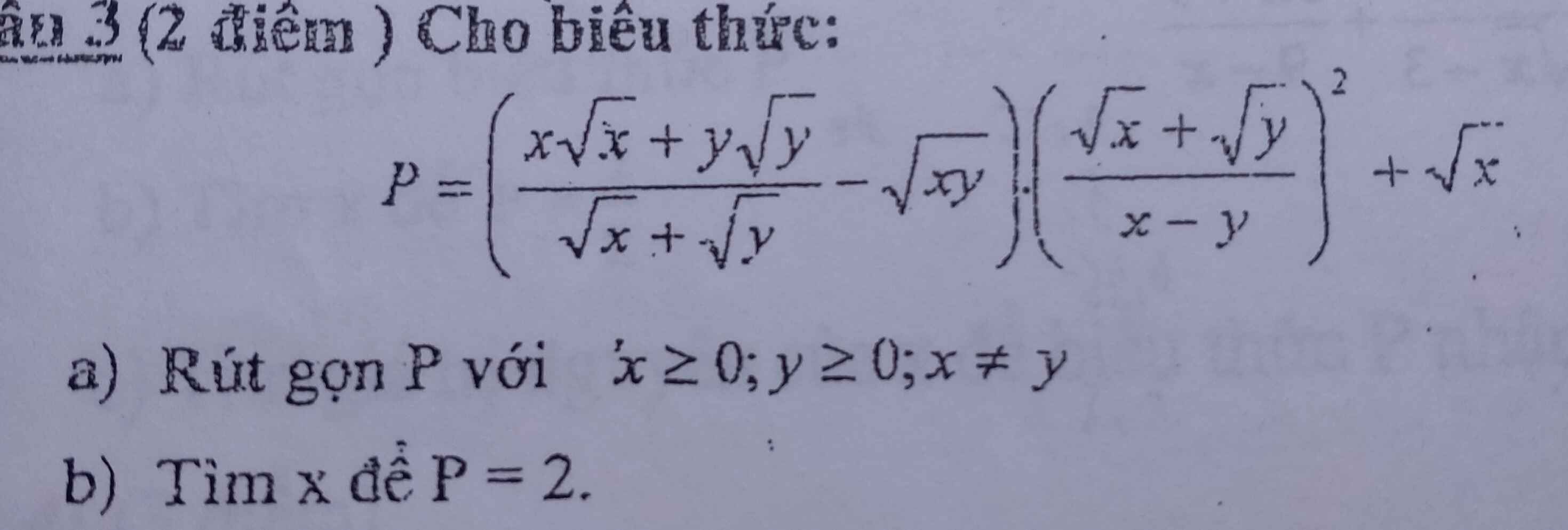a) \(P=\left(\dfrac{x\sqrt{x}+y\sqrt{y}}{\sqrt{x}+\sqrt{y}}\right)\cdot\left(\dfrac{\sqrt{x}+\sqrt{y}}{x-y}\right)^2+\sqrt{x}\)
\(=\left(\dfrac{\sqrt{x^3}+\sqrt{y^3}}{\sqrt{x}+\sqrt{y}}\right)\cdot\left(\dfrac{\sqrt{x}+\sqrt{y}}{\left(\sqrt{x}+\sqrt{y}\right)\cdot\left(\sqrt{x}-\sqrt{y}\right)}\right)^2+\sqrt{x}\)
\(=\left(\dfrac{\left(\sqrt{x}+\sqrt{y}\right)\cdot\left(x-2\sqrt{xy}+y\right)}{\sqrt{x}+\sqrt{y}}\right)\cdot\dfrac{1}{\left(\sqrt{x}-\sqrt{y}\right)^2}+\sqrt{x}\)
\(=\left(x-2\sqrt{xy}+y\right)\cdot\dfrac{1}{x-2\sqrt{xy}+y}+\sqrt{x}\)
\(=\sqrt{x}+1\)
Vậy \(P=\sqrt{x}+1\) với \(x\ge0;y\ge0;x\ne y\)
b) Để P = 2
\(\Rightarrow\sqrt{x}+1=2\)
\(\Leftrightarrow\sqrt{x}=1\)
\(\Leftrightarrow x=1\) (thỏa mãn điều kiện)
Vậy P = 2 thì x = 1