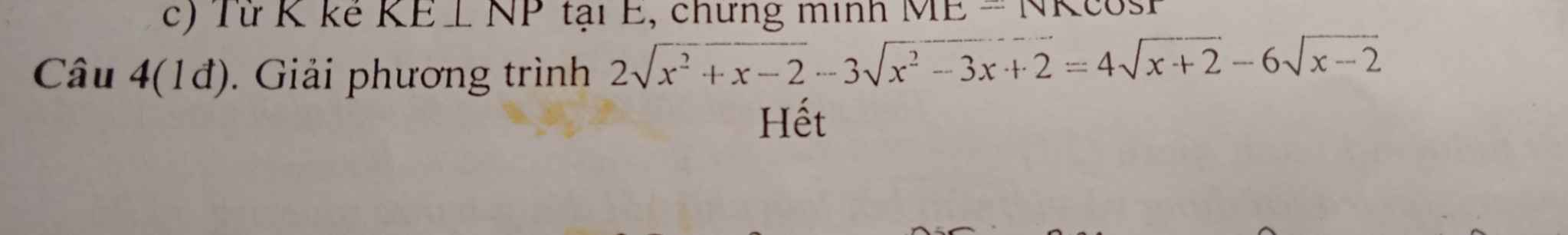Đk:\(x\ge2\)
\(\Leftrightarrow2\sqrt{\left(x+2\right)\left(x-1\right)}-3\sqrt{\left(x-2\right)\left(x-1\right)}=2\left(2\sqrt{x+2}-3\sqrt{x-2}\right)\)
\(\Leftrightarrow\sqrt{x-1}\left(2\sqrt{x+2}-3\sqrt{x-2}\right)=2\left(2\sqrt{x+2}-3\sqrt{x-2}\right)\)
\(\Leftrightarrow\left(\sqrt{x-1}-2\right)\left(2\sqrt{x+2}-3\sqrt{x-2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-1}=2\\2\sqrt{x+2}=3\sqrt{x-2}\end{matrix}\right.\)
\(\cdot\sqrt{x-1}=2\Leftrightarrow x=5\)
\(\cdot2\sqrt{x+2}=3\sqrt{x-2}\)
\(\Leftrightarrow4\left(x+2\right)=9\left(x-2\right)\)
\(\Leftrightarrow x=\dfrac{26}{5}\)
Vậy pt có 2 nghiệm x=5 và x=26\5
Đúng 0
Bình luận (0)
