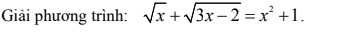ĐK:\(x\ge\dfrac{2}{3}\)
\(\Leftrightarrow\left(3x-2-\sqrt{3x-2}\right)+\left(x-\sqrt{x}\right)+\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow\dfrac{3\sqrt{3x-2}\left(x-1\right)}{\sqrt{3x-2}+1}+\dfrac{\sqrt{x}\left(x-1\right)}{\sqrt{x}+1}+\left(x-3\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(\dfrac{3\sqrt{3x-2}}{\sqrt{3x-2}+1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}+x-3\right)=0\left(\cdot\right)\)
Đặt cái ngoặc to là M
Ta có nhậc xét sau:
\(M=\left(\dfrac{3\sqrt{3x-2}}{\sqrt{3x-2}+1}-\dfrac{3}{2}\right)+\left(\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{1}{2}\right)+\left(x-1\right)=\dfrac{3\sqrt{3x-2}-3}{2\left(\sqrt{3x-2}+1\right)}+\dfrac{\sqrt{x}-1}{2\left(\sqrt{x}+1\right)}+\left(x-1\right)\)
\(=\dfrac{3\left(x-1\right)}{2\left(\sqrt{3x-2}+1\right)^2}+\dfrac{x-1}{2\left(\sqrt{x}+1\right)^2}+x-1=\left(x-1\right)\left(\dfrac{3}{2\left(\sqrt{3x-2}+1\right)^2}+\dfrac{1}{2\left(\sqrt{x}+1\right)}+1\right)\)
Do đó:
\(\left(\cdot\right)\Leftrightarrow\left(x-1\right)^2\left(\dfrac{3}{2\left(\sqrt{3x-2}+1\right)^2}+\dfrac{1}{2\left(\sqrt{x}+1\right)^2}+1\right)=0\)
\(\Leftrightarrow x=1\) (cái ngoặc to lớn 0 với mọi thõa đk)