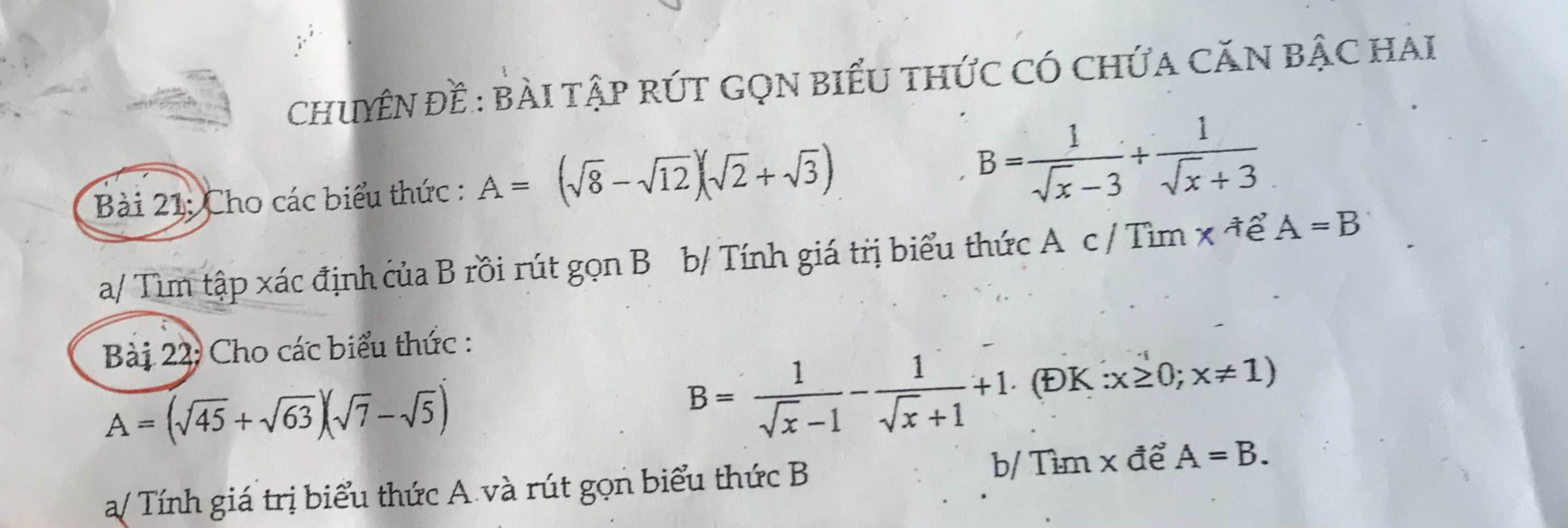Question

Answer 1

Bài 22:

a) Ta có: \(A=\left(\sqrt{45}+\sqrt{63}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
                   \(=\left(3\sqrt{5}+3\sqrt{7}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
                   \(=3\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
                   \(=3\left(7-5\right)\)
                   \(=3.2\)
                   \(=6\)

Với \(x\ge0;x\ne1\) ta có:
\(B=\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}+1}+1\)
    \(=\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
   
    \(=\dfrac{\left(\sqrt{x}+1\right)-\left(\sqrt{x}-1\right)+\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
    \(=\dfrac{2+\left(x-1\right)}{x-1}\)
    \(=\dfrac{1+x}{x-1}\)

Vậy .......

b) Để A = B thì: \(6=\dfrac{1+x}{x-1}\)
                     \(\Rightarrow6x-6=1+x\)
                     \(\Leftrightarrow5x=7\)
                     \(\Leftrightarrow x=\dfrac{7}{5}\) (thỏa mãn)
Vậy.....

Answer 2

Bài 21:

a) Điều kiện xác định của B:
\(\left\{{}\begin{matrix}x>0\\\sqrt{x}-3\ne0\\\sqrt{x}+3\ne0\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}x>0\\\sqrt{x}\ne3\\\sqrt{x}\ne-3 \left(luôn đúng \forall x>0\right)\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}x>0\\x\ne9\end{matrix}\right.\)

Với x>0; x\(\ne\)9 ta có: \(B=\dfrac{1}{\sqrt{x}-3}+\dfrac{1}{\sqrt{x}+3}\)
                                    \(=\dfrac{\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\dfrac{\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
                                    \(=\dfrac{\left(\sqrt{x}+3\right)+\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
                                    \(=\dfrac{2\sqrt{x}}{x-9}\)
Vậy \(B=\dfrac{2\sqrt{x}}{x-9}\) với x>0; x\(\ne\)9

b) Ta có: \(A=\left(\sqrt{8}-\sqrt{12}\right)\left(\sqrt{2}+\sqrt{3}\right)\)
                  \(=\left(2\sqrt{2}-2\sqrt{3}\right)\left(\sqrt{2}+\sqrt{3}\right)\)
                  \(=2\left(\sqrt{2}-\sqrt{3}\right)\left(\sqrt{2}+\sqrt{3}\right)\)
                  \(=2\left(2-3\right)\)
                  \(=2.\left(-1\right)\)
                  \(=-2\)
Vậy A = - 2

c) Để A = B thì:  \(-2=\dfrac{2\sqrt{x}}{x-9}\)
                      \(\Rightarrow-2x+18=2\sqrt{x}\)
                      \(\Leftrightarrow\left(-2x+18\right)^2=4x\)
                      \(\Leftrightarrow4x^2-72x+324=4x\)
                      \(\Leftrightarrow4x^2-76x+324=0\)
                      \(\Leftrightarrow x^2-19x+81=0\)

Ta có: \(\Delta=\left(-19\right)^2-4.1.81=37>0\)
=> Phương trình có 2 nghiệm phân biệt:
\(x_1=\dfrac{-\left(-19\right)+\sqrt{37}}{2.1}=\dfrac{19+\sqrt{37}}{2}\)(thỏa mãn)
\(x_2=\dfrac{-\left(-19\right)-\sqrt{37}}{2.1}=\dfrac{19-\sqrt{37}}{2}\)(thỏa mãn)
Vậy.....