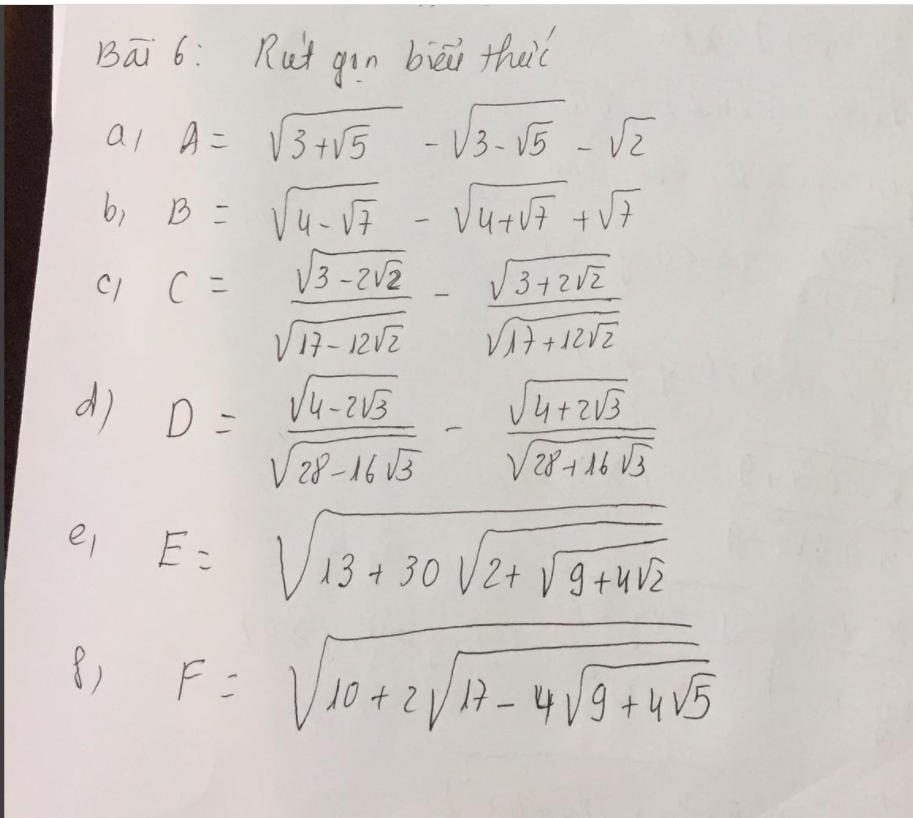Question

Answer 1

a, Ta có :  A=\(\dfrac{\sqrt{6+2\sqrt{5}}}{\sqrt{2}}\) - \(\dfrac{\sqrt{6-2\sqrt{5}}}{\sqrt{2}}\) - \(\sqrt{2}\)  

        <=>  A= \(\sqrt{5}+1\) - (\(\sqrt{5}-1\) ) - \(\sqrt{2}\) 

        <=>  A = 2 - \(\sqrt{2}\) 

        <=>  A= \(\sqrt{2}\)

Answer 2

b, B= \(\dfrac{\sqrt{8-2\sqrt{7}}}{\sqrt{2}}\) - \(\dfrac{\sqrt{8+2\sqrt{5}}}{\sqrt{2}}\) + \(\sqrt{7}\) 

      = \(\sqrt{7}-1\)\(-\left(\sqrt{7}+1\right)\) +\(\sqrt{7}\) 

      = \(\sqrt{7}-2\)