Toán
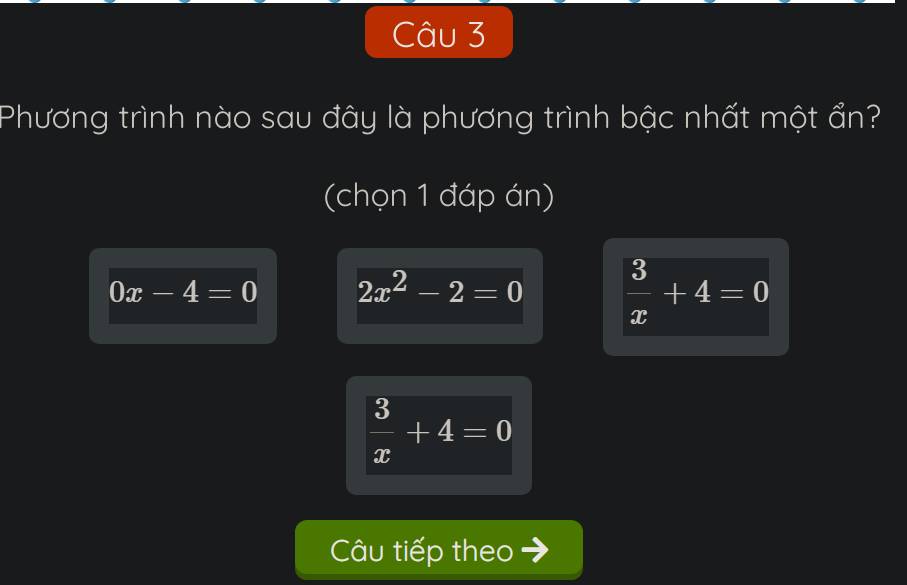
Câu này không có đáp án đúng nha bạn, vì:
+, \(0x-4=-4\) không có bậc
+, \(2x^2-2\) là pt bậc hai một ẩn
+, \(\dfrac{3}{x}+4=3x^{-1}+4\) không có bậc là 1
Đúng 1
Bình luận (1)
1, Trong mặt phẳng tọa độ Oxy cho parabol (P): y = x2 và đường thẳng (d): y = mx + m +1 ( m là tham số )
a, Tìm m đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A,B
1, Quãng sông AB dài 48km. Một ca nô xuôi dòng sông từ A đến B sau đó ngược dòng từ B về A hết 3 giờ 36 phút. Tìm vận tốc riêng của ca nô, biết vận tốc dòng nước là 3km/h.2, Tính diện tích xung quanh và diện tích toàn phần của lon sữa Similac có dạng hình trụ, biết lon sữa có bán kính đáy bằng 5 cm và ciều cao là 10 cm ( lấy π ≈ 3,14 và lết quản làm tròn đến hàng đơn vị )
Đọc tiếp
1, Quãng sông AB dài 48km. Một ca nô xuôi dòng sông từ A đến B sau đó ngược dòng từ B về A hết 3 giờ 36 phút. Tìm vận tốc riêng của ca nô, biết vận tốc dòng nước là 3km/h.
2, Tính diện tích xung quanh và diện tích toàn phần của lon sữa Similac có dạng hình trụ, biết lon sữa có bán kính đáy bằng 5 cm và ciều cao là 10 cm ( lấy π ≈ 3,14 và lết quản làm tròn đến hàng đơn vị )
Cho biểu thức: B =\(\dfrac{\sqrt{x}+2}{\sqrt{x}+1}-\dfrac{3}{\left(\sqrt{x}+1\right)\left(2-\sqrt{x}\right)}\) với x ≥ 0; x ≠ 4
Chứng minh B = \(\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)
Cho phương trình x2 - ( 2m - 1 )x - m =0 với m là tham số.
Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi giá trị của m.
1, Hàng ngày, bạn An đi học từ nhà đến trường bằng xe đạp. Biết rằng khoảng cách từ nhà bạn An đến trường là 4km. Do đó về phải lên dốc nên vận tốc đạp xe chậm hơn vận tốc lúc đi 4km/h, vì vậy thời gian lúc về lâu hơn thời gian lúc đi là 5 phút. Hỏi vận tốc đạp xe lúc về của bạn An bằng bao nhiêu km/h?2, Người ta thiết kế một thùng tôn hình trụ không có nắp để đựng nước có dung tích bằng 2m3. Biết chiều cao thùng tôn là 2m. Hỏi phải dùng tối thiểu bao nhiêu m2 tôn ( không kể mép nối ) để làm đượ...
Đọc tiếp
1, Hàng ngày, bạn An đi học từ nhà đến trường bằng xe đạp. Biết rằng khoảng cách từ nhà bạn An đến trường là 4km. Do đó về phải lên dốc nên vận tốc đạp xe chậm hơn vận tốc lúc đi 4km/h, vì vậy thời gian lúc về lâu hơn thời gian lúc đi là 5 phút. Hỏi vận tốc đạp xe lúc về của bạn An bằng bao nhiêu km/h?
2, Người ta thiết kế một thùng tôn hình trụ không có nắp để đựng nước có dung tích bằng 2m3. Biết chiều cao thùng tôn là 2m. Hỏi phải dùng tối thiểu bao nhiêu m2 tôn ( không kể mép nối ) để làm được thùng tôn trên? Lấy π ≈ 3,14 và kết quả làm tròn đến chữ số thập phân thứ hai.
chứng tỏ rằng : 1/2^2+1/3^2+.....+1/100^2<3/4
ai giúp mik với mik sắp thi rồi
Cho biểu thức: \(\dfrac{\sqrt{x}+3}{x-4}-\dfrac{\sqrt{x}}{x+2\sqrt{x}}-\dfrac{1}{\sqrt{x}-2}\) ( với x > 0; x ≠ 4 )
Rút gọn biểu thức
-5/7 . 3/13 - 5/7 . 10/13 + 1 và 5/7
tính hợp lí
Cho phương trình x2 + mx - m - 1 =0 với m là tham số
a, Giải phương trình khi m = 2
b, Tìm m để phương trình có hai nghiệm phân biệt x1, x2 sao cho tồng bình phương hai nghiệm không vượt quá 2









