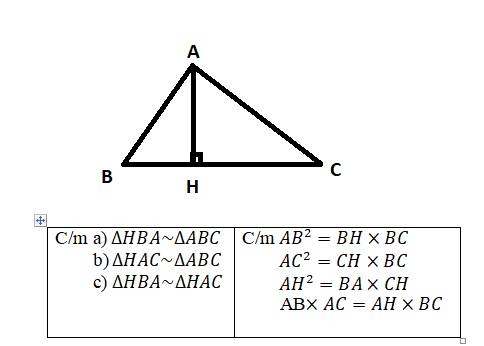
cho tam giác ABC vuông tại A có AB=6cm ,AC=8cm. đường cao AH và phân giác BDcắt nhau tại I (H trên BC và D trên AC)
a)tính độ dài AD,DC
b)Chướng minh tam giác ABC đồng dạng tam giác HBA và AB2=BH.BC
c)chứng minh tam giác ABI đồng dang với tam giác CBD