Bài 4: Khái niệm hai tam giác đồng dạng
Nội dung lý thuyết
1. Tam giác đồng dạng
a) Định nghĩa:
Tam giác \(A'B'C'\) gọi là đồng dạng với tam giác \(ABC\) nếu:
\(\widehat{A'}=\widehat{A}\) ; \(\widehat{B'}=\widehat{B}\) ; \(\widehat{C'}=\widehat{C}\) ;
\(\dfrac{A'B'}{AB}=\dfrac{B'C'}{BC}=\dfrac{A'C'}{AC}\).
Trong đó: \(\widehat{A'}\) và \(\widehat{A}\) ; \(\widehat{B'}\) và \(\widehat{B}\) ; \(\widehat{C'}\) và \(\widehat{C}\) được gọi là các góc tương ứng (hay các đỉnh tương ứng);
\(A'B'\) và \(AB\) ; \(A'C'\) và \(AC\) ; \(B'C'\) và \(BC\) được gọi là các cạnh tương ứng.
Chú ý: Khi kí hiệu 2 tam giác đồng dạng, ta cần viết đúng thứ tự các góc tương ứng.
Ví dụ:
+) \(\Delta HIK\) đồng dạng với \(\Delta MNP\) nếu:
\(\widehat{H}=\widehat{M};\widehat{I}=\widehat{N};\widehat{K}=\widehat{P}\) và \(\dfrac{HI}{MN}=\dfrac{IK}{NP}=\dfrac{HK}{MP}\)
+) \(\Delta DEF\) đồng dạng với \(\Delta D'E'F'\) nếu:
\(\widehat{D}=\widehat{D'}\) ; \(\widehat{E}=\widehat{E'}\) ; \(\widehat{F}=\widehat{F'}\) và \(\dfrac{DE}{D'E'}=\dfrac{EF}{E'F'}=\dfrac{DF}{D'F'}\)
Chú ý: Khi \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\) thì tỉ số các cạnh tương ứng \(\dfrac{A'B'}{AB}=\dfrac{B'C'}{BC}=\dfrac{A'C'}{AC}=k\) được gọi là tỉ số đồng dạng.
Ví dụ 1: Cho \(\Delta ABC\) và \(\Delta A'B'C'\) như sau:

Ta thấy: \(\widehat{A'}=\widehat{A}\) ; \(\widehat{B'}=\widehat{B}\) ; \(\widehat{C'}=\widehat{C}\)
\(\dfrac{A'B'}{AB}=\dfrac{2}{4}=\dfrac{1}{2}\) ; \(\dfrac{A'C'}{AC}=\dfrac{2,5}{5}=\dfrac{1}{2}\) ; \(\dfrac{B'C'}{BC}=\dfrac{3}{6}=\dfrac{1}{2}\)
\(\Rightarrow\) \(\dfrac{A'B'}{AB}=\dfrac{B'C'}{BC}=\dfrac{A'C'}{AC}=\dfrac{1}{2}\)
Ta nói rằng \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\) theo tỉ số \(k=\dfrac{1}{2}\).
Ví dụ 2: Cho \(\Delta ABC\) có \(AB=2cm\), \(AC=5cm\), \(BC=6cm\). Biết rằng \(\Delta DEF\) đồng dạng với \(\Delta ABC\) theo tỉ số \(k=3\). Tính độ dài các cạnh của \(\Delta DEF\)?
Giải:
Ta có: \(\Delta DEF\) đồng dạng với \(\Delta ABC\) theo tỉ số \(k=3\)
\(\Rightarrow\) \(\dfrac{DE}{AB}=\dfrac{EF}{BC}=\dfrac{DF}{AC}=3\)
\(\Rightarrow\left\{{}\begin{matrix}DE=3.AB=3.2=6\left(cm\right)\\EF=3.BC=3.6=18\left(cm\right)\\DF=3.AC=3.5=15\left(cm\right)\end{matrix}\right.\)
Ví dụ 3: Cho \(\Delta DEF\) và \(\Delta MNP\) là hai tam giác đồng dạng. Biết rằng \(DE=6cm\), \(EF=10cm\), \(DF=15cm\) và cạnh lớn nhất của \(\Delta MNP\) là 7,5cm. Tính các cạnh còn lại của \(\Delta MNP\)?
Giải:
Ta có: \(\Delta DEF\) đồng dạng với \(\Delta MNP\)
\(\Rightarrow\) \(\dfrac{DE}{MN}=\dfrac{EF}{NP}=\dfrac{DF}{MP}=k\)
Lại có: \(DF\) là cạnh lớn nhất trong \(\Delta DEF\) suy ra \(MP\) là cạnh lớn nhất trong \(\Delta MNP\).
\(\Rightarrow MP=7,5\left(cm\right)\)
Khi đó ta suy ra tỉ số đồng dạng \(k=\dfrac{15}{7,5}=2\)
\(\Rightarrow\) \(\left\{{}\begin{matrix}\dfrac{DE}{MN}=2\Rightarrow MN=\dfrac{DE}{2}=\dfrac{6}{2}=3\left(cm\right)\\\dfrac{EF}{NP}=2\Rightarrow NP=\dfrac{EF}{2}=\dfrac{10}{2}=5\left(cm\right)\end{matrix}\right.\)
Vậy trong \(\Delta MNP\) có \(MN=3cm\), \(NP=5cm\), \(MP=7,5cm\).
@1492153@
b) Tính chất:
- Tính chất 1: Mỗi tam giác đồng dạng với chính nó (tỉ số đồng dạng là \(k=1\)).
Từ đó ta suy ra: Hai tam giác bằng nhau thì đồng dạng với nhau theo tỉ số đồng dạng \(k=1\)
Ví dụ: \(\Delta ABC=\Delta A'B'C'\) thì ta nói \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\) theo tỉ số \(k=1\).
- Tính chất 2: Nếu \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\) theo tỉ số \(k\) thì \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\) theo tỉ số \(\dfrac{1}{k}\). Ta cũng nói rằng hai tam giác \(\Delta ABC\) và \(\Delta A'B'C'\) đồng dạng với nhau.
Ví dụ: Nếu \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\) theo tỉ số \(k=3\)
thì \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\) theo tỉ số \(k'=\dfrac{1}{3}\).
- Tính chất 3: Nếu \(\Delta A'B'C'\) đồng dạng với \(\Delta A"B"C"\) theo tỉ số \(k_1\) và \(\Delta A"B"C"\) đồng dạng với \(\Delta ABC\) theo tỉ số \(k_2\) thì \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\) theo tỉ số \(k=k_1.k_2\).
Ví dụ: Nếu \(\Delta DEF\) đồng dạng với \(\Delta HIK\) theo tỉ số \(k_1=\dfrac{1}{2}\)
và \(\Delta HIK\) đồng dạng với \(\Delta MNP\) theo tỉ số \(k_2=\dfrac{3}{4}\)
thì \(\Delta DEF\) đồng dạng với \(\Delta MNP\) theo tỉ số \(k=\dfrac{1}{2}.\dfrac{3}{4}=\dfrac{3}{8}\).
- Mở rộng: Nếu hai tam giác đồng dạng với nhau theo tỉ số \(k\) thì chu vi của chúng cũng tỉ lệ với nhau theo tỉ số \(k\).
Ví dụ: Nếu \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\) theo tỉ số \(k=2,5\) thì \(\dfrac{P_{\Delta A'B'C'}}{P_{\Delta ABC}}=2,5\) (P là chu vi tam giác).
Ví dụ: Cho \(\Delta ABC\) đồng dạng với \(\Delta MNP\) theo tỉ số \(\dfrac{2}{3}\), biết chu vi \(\Delta ABC\) là 40cm. Tính chu vi \(\Delta MNP\)?
Giải:
Do \(\Delta ABC\) đồng dạng với \(\Delta MNP\) theo tỉ số \(\dfrac{2}{3}\)
\(\Rightarrow\dfrac{P_{\Delta ABC}}{P_{\Delta MNP}}=\dfrac{2}{3}\) mà \(P_{\Delta ABC}=40\left(cm\right)\)
\(\Rightarrow P_{\Delta MNP}=40:\dfrac{2}{3}=60\left(cm\right)\).
@1492237@
2. Định lí:
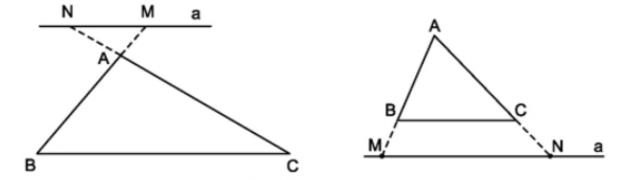
Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
| GT | \(\Delta ABC\), \(MN\) // \(BC\) (\(M\in AB,N\in AC\)) |
| KL | \(\Delta AMN\) đồng dạng với \(\Delta ABC\) |
Chứng minh định lí:

Do \(MN\)//\(BC\) \(\Rightarrow\) \(\widehat{AMN}=\widehat{ABC}\) và \(\widehat{ANM}=\widehat{ACB}\) (cặp góc đồng vị)
Mặt khác: Theo hệ quả của định lí Ta-lét ta có: \(\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}\)
Xét \(\Delta AMN\) và \(\Delta ABC\) có:
\(\widehat{AMN}=\widehat{ABC}\) ; \(\widehat{ANM}=\widehat{ACB}\) ; \(\widehat{A}\) chung
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}\)
Suy ra \(\Delta AMN\) đồng dạng với \(\Delta ABC\).
- Chú ý: Định lí trên cũng đúng trong trường hợp đường thẳng cắt phần kéo dài hai cạnh của tam giác và song song với cạnh còn lại.
Ví dụ 1: Cho hình thang \(ABCD\) (\(AB\)//\(CD\)) có \(AB=10cm\), \(CD=25cm\). Hai đường chéo \(AC,BD\) cắt nhau tại \(O\). Xác định cặp tam giác đồng dạng và tỉ số đồng dạng của chúng?
Giải:
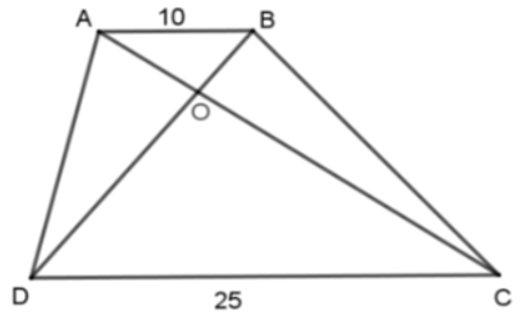
Do \(AB\)//\(CD\) nên áp dụng định lí trên trong tam giác \(OCD\) suy ra \(\Delta OAB\) đồng dạng với \(\Delta OCD\)
\(\Rightarrow\) \(\dfrac{OA}{OC}=\dfrac{OB}{OD}=\dfrac{AB}{CD}=\dfrac{10}{25}=\dfrac{2}{5}\)
Vậy \(\Delta OAB\) đồng dạng với \(\Delta OCD\) theo tỉ số \(\dfrac{2}{5}\).