Bài 1: Định lý Talet trong tam giác

1. Tỉ số của hai đoạn thẳng

Định nghĩa:

Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.

Tỉ số của hai đoạn thẳng \(AB\) và \(CD\) được kí hiệu là \(\dfrac{AB}{CD}\).

Ví dụ: +) Nếu \(AB=3cm\), \(CD=7cm\) thì \(\dfrac{AB}{CD}=\dfrac{3}{7}\).

          +) Nếu \(EF=4dm\), \(MN=9dm\) thì \(\dfrac{EF}{MN}=\dfrac{4}{9}\).

          +) Nếu \(HK=5cm\); \(PQ=3dm\) thì \(\dfrac{HK}{PQ}=\dfrac{5}{30}=\dfrac{1}{6}\) (do \(3dm=30cm\))

Chú ý: Tỉ số của hai đoạn thẳng không phụ thuộc vào cách chọn đơn vị đo.

Ví dụ 1: Cho hai đoạn thẳng \(AB\) và \(CD\), biết \(\dfrac{AB}{CD}=\dfrac{3}{8}\) và \(CD=10cm\). Tính \(AB\)?

Giải:

Ta có: \(\dfrac{AB}{CD}=\dfrac{3}{8}\) \(\Rightarrow\dfrac{AB}{10}=\dfrac{3}{8}\) \(\Rightarrow AB=\dfrac{3.10}{8}\)

          \(\Rightarrow AB=\dfrac{30}{8}=3,75\) (cm)

Vậy độ dài đoạn thẳng AB là 3,75cm.

Ví dụ 2: Cho 2 đoạn thẳng \(DE\) và \(MN\). Biết hai đoạn thẳng tỉ lệ với 2:5 và \(MN\) dài hơn \(DE\) là 12dm. Tính độ dài mỗi đoạn thẳng?

Giải:

Ta có: \(\left\{{}\begin{matrix}\dfrac{DE}{MN}=\dfrac{2}{5}\\MN-DE=12\left(cm\right)\end{matrix}\right.\)  

\(\Rightarrow MN=\dfrac{12}{5-2}.5=\dfrac{12}{3}.5=4.5=20\left(cm\right)\)

\(\Rightarrow DE=\dfrac{2}{5}.20=8\left(cm\right)\)

Vậy độ dài \(DE\) và \(MN\) lần lượt là \(8cm;20cm\).

2. Đoạn thẳng tỉ lệ

Định nghĩa:

Hai đoạn thẳng \(AB\) và \(CD\) gọi là tỉ lệ với hai đoạn thẳng \(A'B'\) và \(C'D'\) nếu có tỉ lệ thức: \(\dfrac{AB}{CD}=\dfrac{A'B'}{C'D'}\) hay \(\dfrac{AB}{A'B'}=\dfrac{CD}{C'D'}\).

Ví dụ 1: Cho 4 đoạn thẳng \(AB,CD,A'B',C'D'\) (hình vẽ)

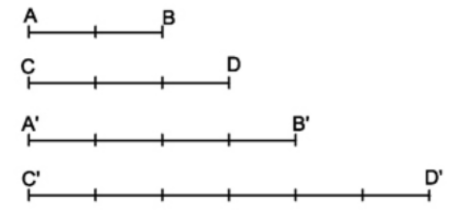
Ta thấy: \(\dfrac{AB}{CD}=\dfrac{2}{3}\); \(\dfrac{A'B'}{C'D'}=\dfrac{4}{6}=\dfrac{2}{3}\) \(\Rightarrow\) \(\dfrac{AB}{CD}=\dfrac{A'B'}{C'D'}\) 

Suy ra 2 đoạn thẳng \(AB\) và \(CD\) tỉ lệ với hai đoạn thẳng \(A'B'\) và \(C'D'\).

Ví dụ 2: Cho đoạn thẳng \(AB=3cm\), \(CD=5dm\), \(GH=x\left(cm\right)\), \(IK=y\left(cm\right)\). Biết rằng hai đoạn thẳng \(AB\) và \(CD\) tỉ lệ với hai đoạn thẳng \(GH\) và \(IK\). Tính tỉ lệ \(\dfrac{x}{y}\)?

Giải:

Đổi \(5dm=50cm\)

Do hai đoạn thẳng \(AB\) và \(CD\) tỉ lệ với hai đoạn thẳng \(GH\) và \(IK\) nên ta có: \(\dfrac{AB}{CD}=\dfrac{GH}{IK}\)

 \(\Rightarrow\dfrac{3}{50}=\dfrac{x}{y}\)

Vậy \(\dfrac{x}{y}=\dfrac{3}{50}\).

3. Định lí Ta-lét trong tam giác

Định lí Ta-lét: (Thừa nhận, không chứng minh)

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Hình vẽ: 

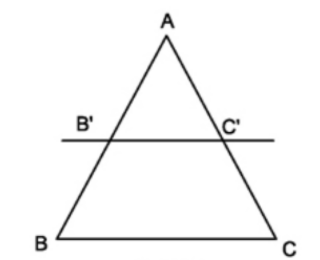
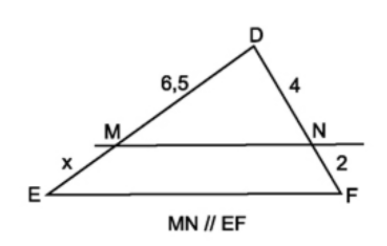
Ví dụ 1: Cho hình vẽ. Biết rằng \(MN\)//\(EF\). Tính \(x\)?

Giải:

Do \(MN\)//\(EF\) nên theo định lí Ta-lét ta có: \(\dfrac{DM}{ME}=\dfrac{DN}{NF}\)

\(\Rightarrow\dfrac{6,5}{x}=\dfrac{4}{2}\) \(\Rightarrow x=\dfrac{2.6,5}{4}=3,25\)

Vậy \(x=3,25\).

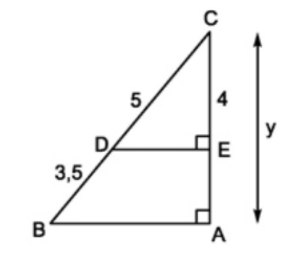
Ví dụ 2. Cho hình vẽ. Tính \(y\)?

Giải:

Ta có: \(DE\perp AC\), \(AB\perp AC\) \(\Rightarrow\) \(DE\) // \(AB\) (từ vuông góc đến song song)

Theo định lí Ta-lét ta có: \(\dfrac{CD}{DB}=\dfrac{CE}{EA}\)

\(\Rightarrow\) \(\dfrac{5}{3,5}=\dfrac{4}{EA}\) \(\Rightarrow EA=\dfrac{4.3,5}{5}=2,8\)

Khi đó: \(AC=CE+EA=4+2,8=6,8\)

Hay \(y=6,8\).

Ví dụ 3: Cho hình vẽ. Tính giá trị của biểu thức \(x-y\)?

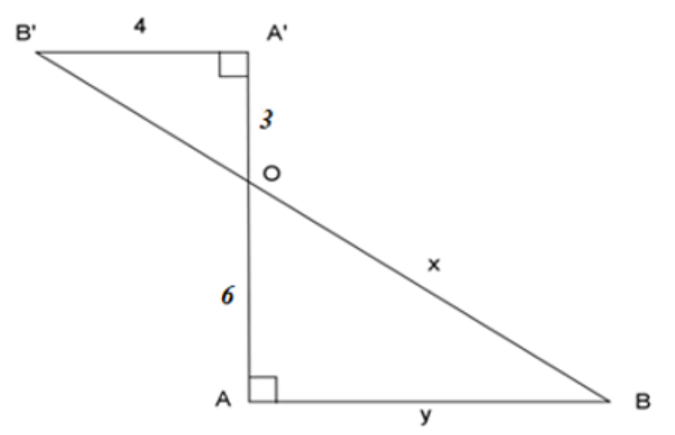
Giải:

Áp dụng định lí Py-ta-go trong tam giac vuông \(OA'B'\) ta có: \(OA'^2+A'B'^2=OB'^2\)

\(\Rightarrow OB'^2=3^2+4^2=25\)

\(\Rightarrow OB'=5\)

 Ta có: \(AB\perp AA'\), \(A'B'\perp AA'\) \(\Rightarrow\) \(AB\)//\(A'B'\) (từ vuông góc đến song song)

Theo định lí Ta-lét ta có: \(\dfrac{OA'}{OA}=\dfrac{OB'}{OB}=\dfrac{A'B'}{AB}\)

\(\Rightarrow\dfrac{3}{6}=\dfrac{5}{x}=\dfrac{4}{y}\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{5}{x}=\dfrac{3}{6}=\dfrac{1}{2}\\\dfrac{4}{y}=\dfrac{3}{6}=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=10\\y=8\end{matrix}\right.\)

Khi đó: \(x-y=10-8=2\)

Vậy \(x-y=2\).