Bài 2: Định lý đảo và hệ quả của định lý Talet
Nội dung lý thuyết
1. Định lí đảo
Định lí Ta-lét đảo (Ta thừa nhận,không chứng minh):
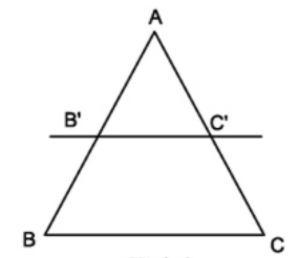
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
| GT | \(\Delta ABC\), \(B'\in AB\), \(C'\in AC\) \(\dfrac{AB'}{B'B}=\dfrac{AC'}{C'C}\) |
| KL | \(B'C'\) // \(BC\) |
Ví dụ 1: Cho tam giác \(ABC\), trên \(AB\), \(AC\), \(BC\) lần lượt lấy \(D,E,F\) (như hình vẽ).
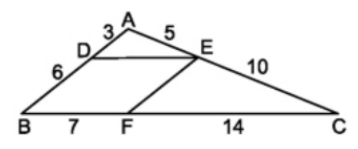
a) Chỉ ra các cặp đường thẳng song song?
b) So sánh các tỉ số \(\dfrac{AD}{AB}\) , \(\dfrac{AE}{AC}\), \(\dfrac{DE}{BC}\)?
Giải:
a) Ta có: \(\dfrac{AD}{DB}=\dfrac{3}{6}=\dfrac{1}{2}\), \(\dfrac{AE}{EC}=\dfrac{5}{10}=\dfrac{1}{2}\) \(\Rightarrow\) \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
Xét trong tam giác \(ABC\) có \(D\in AB,E\in AC\) và \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\) .
Áp dụng định lí Ta-lét đảo ta suy ra \(DE\) // \(BC\).
Lại có: \(\dfrac{CE}{EA}=\dfrac{10}{5}=2\), \(\dfrac{CF}{FB}=\dfrac{14}{7}=2\) \(\Rightarrow\) \(\dfrac{CE}{EA}=\dfrac{CF}{FB}\)
Xét trong tam giác \(ABC\) có \(E\in CA,F\in CB\) và \(\dfrac{CE}{EA}=\dfrac{CF}{FB}\)
Áp dụng định lí Ta-lét đảo ta suy ra \(EF\) // \(AB\).
b) Ta có: \(\dfrac{AD}{AB}=\dfrac{3}{3+6}=\dfrac{3}{9}=\dfrac{1}{3}\)
\(\dfrac{AE}{AC}=\dfrac{5}{5+10}=\dfrac{5}{15}=\dfrac{1}{3}\)
Mặt khác, xét tứ giác \(BDEF\) có: \(DE\) // \(BF\) ; \(EF\) // \(BD\)
\(\Rightarrow\) \(BDEF\) là hình bình hành
\(\Rightarrow\) \(DE=BF=7\)
Khi đó: \(\dfrac{DE}{BC}=\dfrac{7}{7+14}=\dfrac{7}{21}=\dfrac{1}{3}\)
Suy ra \(\dfrac{AD}{AB}\)=\(\dfrac{AE}{AC}\)=\(\dfrac{DE}{BC}\).
Ví dụ 2: Chỉ ra các đường thẳng song song với nhau trong hình vẽ dưới đây:
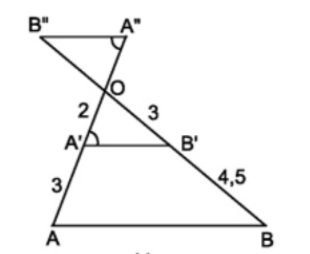
Giải:
Xét đường thẳng \(A'B'\) và \(A"B"\) có:
\(\widehat{B"A"A'}=\widehat{B'A'A"}\) mà 2 góc này ở vị trí so le trong \(\Rightarrow\) \(A'B'\) // \(A"B"\) (1)
Xét trong tam giác \(OAB\) có:
\(A'\in OA,B'\in OB\)
\(\dfrac{OA'}{A'A}=\dfrac{2}{3}\), \(\dfrac{OB'}{B'B}=\dfrac{3}{4,5}=\dfrac{2}{3}\) \(\Rightarrow\) \(\dfrac{OA'}{A'A}=\dfrac{OB'}{B'B}\)
Áp dụng định lí Ta-lét đảo trong \(\Delta OAB\) suy ra \(A'B'\) // \(AB\) (2)
Từ (1) và (2) \(\Rightarrow\) \(AB\) // \(A'B'\) // \(A"B"\).
@1483814@
2. Hệ quả của định lí Ta-lét
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
| GT | \(\Delta ABC\), \(B'C'\) // \(BC\) (\(B'\in AB\), \(C'\in AC\)) |
| KL | \(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}=\dfrac{B'C'}{BC}\) |

Chứng minh:
Vì \(B'C'\) // \(BC\) nên theo định lí Ta-lét ta có: \(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\) (1)
Từ \(C'\) kẻ \(C'D\) // \(AB\) (\(D\in BC\)). Theo định lí Ta-lét ta có: \(\dfrac{AC'}{AC}=\dfrac{BD}{BC}\) (2)
Tứ giác \(B'C'DB\) là hình bình hành (vì có các cặp cạnh đối song song) nên ta có: \(B'C'=BD\)
Từ (1) và (2), thay \(B'C'=BD\) ta có: \(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}=\dfrac{B'C'}{BC}\).
Ví dụ 1: Cho hình vẽ. Biết rằng \(DE\) // \(BC\). Tính \(x\)?

Giải:
Xét trong tam giác \(ABC\) có \(DE\) // \(BC\) (\(D\in AB,E\in AC\))
Áp dụng hệ quả của định lí Ta-lét ta được: \(\dfrac{AD}{AB}=\dfrac{AE}{AC}=\dfrac{DE}{BC}\)
Lại có: \(\dfrac{AD}{AB}=\dfrac{2}{2+3}=\dfrac{2}{5}\)
\(\Rightarrow\dfrac{x}{6,5}=\dfrac{2}{5}\) \(\Rightarrow x=\dfrac{2.6,5}{5}=2,6\)
Vậy \(x=2,6\).
Chú ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng \(a\) song song với một cạnh của tam giác và cắt phần kéo dài của hai cạnh còn lại.
\(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}=\dfrac{B'C'}{BC}\)

Ví dụ 2: Cho hình vẽ, biết rằng \(MN\)//\(PQ\). Tính \(x\)?

Giải:
Xét tam giác \(OPQ\) có \(MN\) // \(PQ\) (\(M\in OQ,N\in OP\))
Áp dụng hệ quả của định lí Ta-lét ta có: \(\dfrac{ON}{OP}=\dfrac{OM}{OQ}=\dfrac{MN}{PQ}\)
Suy ra \(\dfrac{3}{5,2}=\dfrac{2}{x}\) \(\Rightarrow x=\dfrac{2.5,2}{3}\approx3,47\)
@58552@