Bài 6: Trường hợp đồng dạng thứ hai

1. Định lí

Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng.

Chứng minh định lí:

Trên tia \(AB\) lấy đoạn \(AM=A'B'\). Qua \(M\) kẻ \(MN\)//\(BC\) (\(N\in AC\))

Ta có: \(\Delta AMN\) đồng dạng với \(\Delta ABC\) \(\Rightarrow\) \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)

Vì \(AM=A'B'\) \(\Rightarrow\) \(\dfrac{A'B'}{AB}=\dfrac{AN}{AC}\)

Do \(\dfrac{A'B'}{AB}=\dfrac{A'C'}{AC}\) (gt) \(\Rightarrow\) \(\dfrac{A'C'}{AC}=\dfrac{AN}{AC}\) \(\Rightarrow A'C'=AN\)

Khi đó ta suy ra \(\Delta AMN=\Delta A'B'C'\) (c.g.c)

Mà \(\Delta AMN\) đồng dạng với \(\Delta ABC\) \(\Rightarrow\) \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\).

Ví dụ:

+) Nếu \(\Delta ABC\) và \(\Delta DEF\) có \(\dfrac{AB}{DE}=\dfrac{BC}{EF}\) và \(\widehat{B}=\widehat{E}\) thì \(\Delta ABC\) đồng dạng với \(\Delta DEF\);

+) Nếu \(\Delta HIK\) và \(\Delta MNP\) có \(\dfrac{HK}{MP}=\dfrac{IK}{NP}\) và \(\widehat{K}=\widehat{P}\) thì \(\Delta HIK\) đồng dạng với \(\Delta MNP\);

+) Nếu \(\Delta RSK\) và \(\Delta PQM\) có \(\dfrac{RS}{MP}=\dfrac{RK}{MQ}\) và \(\widehat{R}=\widehat{M}\) thì \(\Delta RSK\) đồng dạng với \(\Delta MPQ\).

2. Áp dụng

Ví dụ 1: Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có các số đo như hình vẽ:

Ta có: \(\dfrac{AB}{DE}=\dfrac{4}{8}=\dfrac{1}{2}\) ; \(\dfrac{AC}{DF}=\dfrac{3}{6}=\dfrac{1}{2}\) \(\Rightarrow\) \(\dfrac{AB}{DE}=\dfrac{AC}{DF}\)

        Và \(\widehat{A}=\widehat{D}=60^0\)

\(\Rightarrow\) \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\) (c.g.c)

Ví dụ 2: Cho tam giác \(ABC\) có \(AB=8cm\), \(AC=12cm\). Trên \(AB,AC\) lần lượt lấy điểm \(M,N\) sao cho \(AM=6cm\), \(AN=4cm\). Biết \(MN=8cm.\) Tính \(BC\)?

Giải:

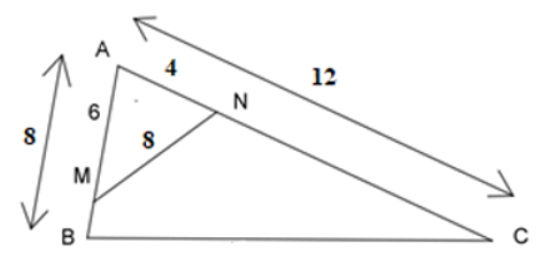
Ta có: \(\dfrac{AN}{AB}=\dfrac{4}{8}=\dfrac{1}{2}\) ; \(\dfrac{AM}{AC}=\dfrac{6}{12}=\dfrac{1}{2}\) \(\Rightarrow\) \(\dfrac{AN}{AB}=\dfrac{AM}{AC}\)

Xét \(\Delta AMN\) và \(\Delta ACB\) có:

          \(\dfrac{AN}{AB}=\dfrac{AM}{AC}\) 

           \(\widehat{A}\) chung

\(\Rightarrow\) \(\Delta AMN\) đồng dạng với \(\Delta ACB\) (c.g.c)

\(\Rightarrow\) \(\dfrac{AN}{AB}=\dfrac{AM}{AC}=\dfrac{MN}{BC}=\dfrac{1}{2}\) 

\(\Rightarrow\) \(\dfrac{8}{BC}=\dfrac{1}{2}\Rightarrow BC=16\left(cm\right)\)

Ví dụ 3: Cho hình thang \(ABCD\) (\(AB\)//\(CD\)) có \(AB=4\), \(CD=16\), \(AD=12\), \(AC=8\). Tính độ dài \(BC\) ?

Giải:

Ta có: \(\dfrac{AB}{AC}=\dfrac{4}{8}=\dfrac{1}{2}\) ; \(\dfrac{AC}{CD}=\dfrac{8}{16}=\dfrac{1}{2}\) \(\Rightarrow\) \(\dfrac{AB}{AC}=\dfrac{AC}{DC}=\dfrac{1}{2}\)

Xét \(\Delta ABC\) và \(\Delta CAD\) có:

           \(\dfrac{AB}{AC}=\dfrac{AC}{DC}=\dfrac{1}{2}\) 

            \(\widehat{BAC}=\widehat{ACD}\) (hai góc so le trong)

\(\Rightarrow\) \(\Delta ABC\) đồng dạng với \(\Delta CAD\) (c.g.c)

\(\Rightarrow\) \(\dfrac{AB}{AC}=\dfrac{AC}{DC}=\dfrac{BC}{AD}=\dfrac{1}{2}\)

\(\Rightarrow\) \(\dfrac{BC}{12}=\dfrac{1}{2}\Rightarrow BC=6\)

Vậy \(BC=6\).

Ví dụ 4: Cho tam giác \(ABC\) có \(AB=9cm,BC=7cm,AC=12cm\).

            Chứng minh rằng: \(\widehat{B}=2.\widehat{C}\)?

Giải:

Trên tia đối của tia \(BA\) lấy điểm \(D\) sao cho \(BD=BC=7cm\)

Ta có: \(\dfrac{AB}{AC}=\dfrac{9}{12}=\dfrac{3}{4}\) ; \(\dfrac{AC}{AD}=\dfrac{12}{9+7}=\dfrac{12}{16}=\dfrac{3}{4}\) \(\Rightarrow\) \(\dfrac{AB}{AC}=\dfrac{AC}{AD}\)

Xét \(\Delta ABC\) và \(\Delta ACD\) có:

           \(\dfrac{AB}{AC}=\dfrac{AC}{AD}\) (cmt)

            \(\widehat{A}\) chung

\(\Rightarrow\) \(\Delta ABC\) đồng dạng với \(\Delta ACD\)

\(\Rightarrow\widehat{ACB}=\widehat{ADC}\)

Lại có: \(\Delta BCD\) cân tại \(B\) (do \(BD=BC=7cm\))

\(\Rightarrow\widehat{BCD}=\widehat{BDC}=\widehat{ADC}\)

Do đó: \(\widehat{BCD}=\widehat{BDC}=\widehat{ADC}=\widehat{ACB}\) 

Ta có: \(\widehat{CBA}\) là góc ngoài đỉnh \(B\) của tam giác \(BCD\)

nên \(\widehat{CBA}=\widehat{BCD}+\widehat{BDC}=2.\widehat{ACB}\) 

Vậy xét trong \(\Delta ABC\) ta có \(\widehat{B}=2.\widehat{C}\).