Bài 2:
a: \(x^4-7x^2+1\)
\(=x^4+2x^2+1-9x^2\)
\(=\left(x^2+1\right)^2-\left(3x\right)^2\)
\(=\left(x^2+1-3x\right)\left(x^2+1+3x\right)\)
b:
b1: ĐKXĐ: \(x\notin\left\{-3;-2;1\right\}\)
b2: \(A=\left(\dfrac{2-x}{x+3}-\dfrac{3-x}{x+2}+\dfrac{2-x}{x^2+5x+6}\right):\left(1-\dfrac{x}{x-1}\right)\)
\(=\left(\dfrac{-\left(x-2\right)}{x+3}+\dfrac{x-3}{x+2}+\dfrac{2-x}{\left(x+2\right)\left(x+3\right)}\right):\dfrac{x-1-x}{x-1}\)
\(=\dfrac{-\left(x-2\right)\left(x+2\right)+\left(x-3\right)\left(x+3\right)+2-x}{\left(x+3\right)\left(x+2\right)}\cdot\dfrac{x-1}{-1}\)
\(=\dfrac{-x^2+4+x^2-9+2-x}{\left(x+3\right)\left(x+2\right)}\cdot\left(-x+1\right)\)
\(=\dfrac{-x-3}{\left(x+3\right)\left(x+2\right)}\cdot\left(-x+1\right)=\dfrac{-1\cdot\left(-x+1\right)}{x+2}=\dfrac{x-1}{x+2}\)
b3: \(x=\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)\cdot...\cdot\left(1-\dfrac{1}{2024^2}\right)\)
\(=\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{2024}\right)\left(1+\dfrac{1}{2}\right)\cdot\left(1+\dfrac{1}{3}\right)\cdot...\cdot\left(1+\dfrac{1}{2024}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot...\cdot\dfrac{2023}{2024}\cdot\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{2025}{2024}=\dfrac{1}{2024}\cdot\dfrac{2025}{2}=\dfrac{2025}{4048}\)
Khi x=2025/4048 thì \(A=\dfrac{\dfrac{2025}{4048}-1}{\dfrac{2025}{4048}+2}=-\dfrac{2023}{10121}\)
Bài 5:
a: Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
nên ADHE là hình chữ nhật
=>AH=DE
Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{HBA}\right)\)
Do đó: ΔHAB~ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
mà AH=DE
nên \(DE^2=HB\cdot HC\)
b: Xét ΔDAH vuông tại D và ΔDHB vuông tại H có
\(\widehat{DAH}=\widehat{DHB}\left(=90^0-\widehat{HBA}\right)\)
Do đó: ΔDAH~ΔDHB
=>\(\dfrac{DA}{DH}=\dfrac{DH}{DB}\)
=>\(DH^2=DA\cdot DB\)
Xét ΔEAH vuông tại E và ΔEHC vuông tại E có
\(\widehat{EAH}=\widehat{EHC}\left(=90^0-\widehat{C}\right)\)
Do đó: ΔEAH~ΔEHC
=>\(\dfrac{EA}{EH}=\dfrac{EH}{EC}\)
=>\(EH^2=EA\cdot EC\)
ADHE là hình chữ nhật
=>\(HA^2=HD^2+HE^2=DA\cdot DB+EA\cdot EC\)
c: ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=MC=MB
Xét ΔMAC có MA=MC
nên ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{MCA}\)
ADHE là hình chữ nhật
=>\(\widehat{AED}=\widehat{AHD}\)
mà \(\widehat{AHD}=\widehat{ABC}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{AED}=\widehat{ABC}\)
\(\widehat{AED}+\widehat{MAC}=\widehat{ABC}+\widehat{ACB}=90^0\)
=>AM\(\perp\)DE
Đúng 1
Bình luận (0)

Bài 2. Tính chiều rộng của một con sông biết lấy điểm \( A \) ở bờ sông bên kia, điểm \( B \) ở bờ sông bên này thì độ dài đoạn thẳng \( AB \) là chiều rộng của con sông. Trên bờ sông bên này, người ta xác định được 3 điểm \( O, C, E \) sao cho \( OC \) song song với bờ sông \( EB \); \( A, B, C \) thẳng hàng; \( A, E, O \) thẳng hàng (như hình vẽ); và đo được \( BC = 125 \, m, \, BE = 20 \, m, \, OC = 25 \, m \).
Xét \(2\Delta:\Delta ABE\) và \(\Delta ACO\) có:
\(\left\{{}\begin{matrix}\widehat{A}chung\\\widehat{AEB}=\widehat{AOC}\end{matrix}\right.\)
\(\Rightarrow\Delta ABE\sim\Delta ACO\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{EB}{OC}\Leftrightarrow\dfrac{AB}{AB+BC}=\dfrac{EB}{OC}\Leftrightarrow\dfrac{AB}{AB+125}=\dfrac{20}{25}\)
\(\Leftrightarrow AB=500\left(m\right)\)
Đúng 1
Bình luận (0)
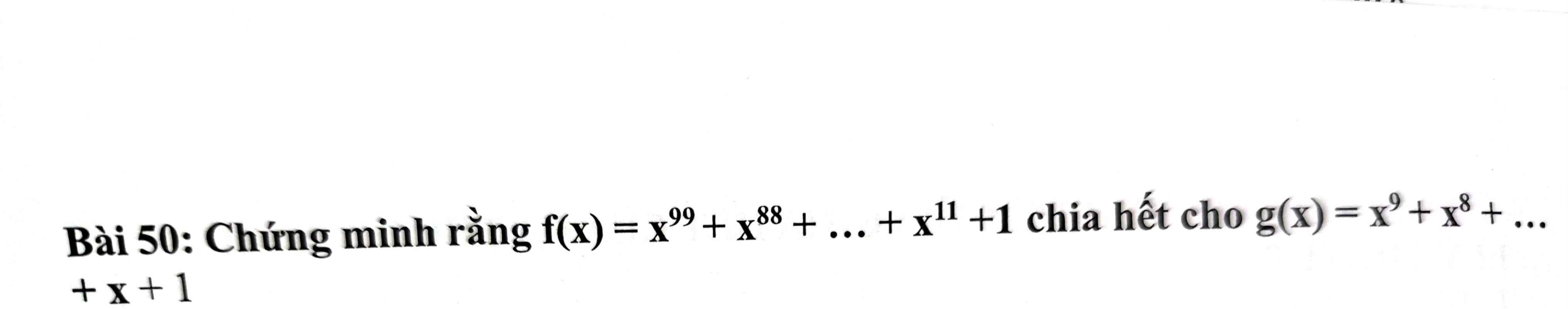 giúp em với ạ
giúp em với ạ
Bài 50: Chứng minh rằng \( f(x) = x^{99} + x^{88} + \ldots + x^{11} + 1 \) chia hết cho \( g(x) = x^9 + x^8 + \ldots + x + 1 \)
Ta có: `f(x) -g(x)=(x^99+x^88+...+x^11+1)-(x^9+x^8+...+x+1)`
`=(x^99-x^9)+(x^88-x^8)+...+(x^11-x)`
`=x^9(x^90-1)+x^8(x^80-1)+...+x(x^10-1)`
Ta có:`x^90-1=(x^10)^9-1^9 \vdots x^10-1` (vì `a^n-b^n \vdots a-b`)
`=> x^80-1 \vdots x^10-1,....,x^10-1 \vdots x^10-1`
`=> f(x)-g(x) \vdots x^10-1`
mà `x^10-1=(x^10+x^9+x^8+...+x^2+x) - (x^9+x^8+...+x+1)=(x-1)(x^9+x^8+...+1)`
`=> x^10-1 \vdots g(x)`
`=> f(x)-g(x) \vdots g(x)`
`=> f(x) \vdots g(x)` `(đpcm)`
Đúng 1
Bình luận (0)
Cho ΔABC, đường cao AH. Biết AH\(^2\) = BH . CH. Cm :
a) ΔHAB ∞ ΔHCA
b) ΔABC ⊥ tại A
a) Ta có :
\(AH^2=BH.CH\)
\(\Rightarrow\dfrac{AH}{BH}=\dfrac{CH}{AH}\)
mà \(\widehat{AHB}=\widehat{AHC}=90^o\) (\(AH\) là đường cao)
\(\Rightarrow\Delta HAB\approx\Delta HCA\left(c.g.c\right)\)
b) Ta có :
\(\Delta HAB\approx\Delta HCA\left(cmt\right)\)
\(\Rightarrow\widehat{BAH}=\widehat{HCA};\widehat{ABH}=\widehat{HAC}\)
mà \(\widehat{ABH}+\widehat{BAH}=90^o\)
\(\widehat{HAC}+\widehat{HCA}=90^o\)
\(\Rightarrow\widehat{BAH}+\widehat{HAC}=90^o\)
\(\Rightarrow\widehat{BAC}=90^o\)
\(\Rightarrow AB\perp AC\)
\(\Rightarrow\Delta ABC\) vuông tại \(A\left(đpcm\right)\)
Đúng 1
Bình luận (0)
Cho ΔABC ∞ ΔMNP.
a) D, Q là trung điểm BC, NP. Cm: ΔABD ∞ ΔMNQ
b) G, K lần lượt là trung điểm ΔABC, ΔMNP. Cm ΔABG ∞ ΔMNK
a, Ta có: `\triangleABC` $\backsim$ `\triangleMNP`
`=> {(\frac{AB}{MN}=\frac{BC}{NP}=\frac{AC}{MP}),(\hat{ABC}=\hat{MNP}),(\hat{BAC}=\hat{NMP}):}`
Vì `D,Q` là trung điểm `BC,NP` nên `\frac{AB}{MN}=\frac{BC}{NP}=\frac{BD}{NQ}`
Xét `\triangleABD` và `\triangleMNQ` có:
`\frac{AB}{MN}=\frac{BD}{NQ}`
`\hat{ABD}=\hat{MNQ}`
`=> \triangleABD` $\backsim$ `\triangleMNQ(c.g.c)` `(đpcm)`
b, ( `G,K` là trung điểm `AC,MP` )
Vì `G,K` là trung điểm `AC,MP` nên `\frac{AB}{MN}=\frac{AC}{MP}=\frac{AG}{MK}`
Xét `\triangleABG` và `\triangleMNK` có:
`\frac{AB}{MN}=\frac{AG}{MK}`
`\hat{BAG}=\hat{NMK}`
`=>\triangleABG` $\backsim$ `\triangleMNK(c.g.c)` `(đpcm)`
Đúng 1
Bình luận (0)
Cho góc DAC < 90\(^o\). Gọi B là hình chiếu của D trên BC sao cho AB = 4cm; BC = 3cm; BD = 6cm; G ∈ AD, CG cắt BD = Esao cho BE = 2cm. CM:
a) ΔABC ∞ ΔEBC
b) góc DAB = góc DEG
c) ΔDGB cân
Cho tg ABCD, AC cắt BD = I sao cho AI = 2cm; IC = 7cm; DI = 4cm; BI = 3,5cm.
CM:
a) ΔIAB ∞ ΔIDC
b) ΔIAD ∞ ΔIBC
a)Xét ΔIAB và ΔIDC:
\(\dfrac{AI}{ID}=\dfrac{2}{4}=\dfrac{1}{2}\)
\(\dfrac{AI}{ID}=\dfrac{2}{4}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AI}{ID}=\dfrac{BI}{IC}\)
\(\widehat{AIB}=\widehat{DIC}\) (đ2)
Do đó, ΔIAB \(\sim\) ΔIDC (c.g.c).
b)Xét ΔIAD và ΔIBC:
\(\dfrac{AI}{IB}=\dfrac{2}{3}.5=\dfrac{4}{7}\)
\(\dfrac{ID}{IC}=\dfrac{4}{7}\)
\(\Rightarrow\dfrac{AI}{IB}=\dfrac{ID}{IC}\)
\(\widehat{AID}=\widehat{BIC}\) (đ2)
Do đó, ΔIAD \(\sim\) ΔIBC (c.g.c).
Đúng 1
Bình luận (1)

13. Cho $\frac{a}{b+c} + \frac{b}{c+a} + \frac{c}{a+b} = 1$. Chứng minh rằng: $\frac{a^2}{b+c} + \frac{b^2}{c+a} + \frac{c^2}{a+b} = 0$
14. Cho $\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$ và $\frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 0$. Chứng minh rằng: $\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1$.
13) Ta có :
\(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}=1\)
\(\Leftrightarrow\left(a+b+c\right)\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)=a+b+c\)
\(\Leftrightarrow\dfrac{a^2+a\left(b+c\right)}{b+c}+\dfrac{b^2+b\left(c+a\right)}{c+a}+\dfrac{c^2+c\left(a+b\right)}{a+b}=a+b+c\)
\(\Leftrightarrow\dfrac{a^2}{b+c}+a+\dfrac{b^2}{c+a}+b+\dfrac{c^2}{a+b}+c=a+b+c\)
\(\Leftrightarrow\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}=0\left(đpcm\right)\)
14) Ta có :
\(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\)
\(\Leftrightarrow\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}+2\left(\dfrac{xy}{ab}+\dfrac{yz}{bc}+\dfrac{xz}{ca}\right)=1\)
Mà \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1\left(gt\right)\)
\(\Leftrightarrow1+2\left(\dfrac{xy}{ab}+\dfrac{yz}{bc}+\dfrac{xz}{ca}\right)=1\)
\(\Leftrightarrow\dfrac{xy}{ab}+\dfrac{yz}{bc}+\dfrac{xz}{ca}=0\)
\(\Leftrightarrow xyc+yza+xzb=0\left(a;b;c\ne0\right)\)
\(\Leftrightarrow\dfrac{c}{z}+\dfrac{a}{x}+\dfrac{b}{y}=0\left(x;y;z\ne0\right)\)
hay \(\dfrac{a}{x}+\dfrac{b}{y}+\dfrac{c}{z}=0\left(đpcm\right)\)
Đúng 1
Bình luận (0)
 giúp tớ với
giúp tớ với
Bài 8: Cho tam giác \(ABC\) cân tại \(A \left(\hat{A} < 90^\circ \right)\), các đường cao \(BD\) và \(CE\) cắt nhau tại \(H\). Tia phân giác của góc \(ABD\) cắt \(EC\) và \(AC\) theo thứ tự tại \(M\) và \(P\). Tia phân giác của góc \(ACE\) cắt \(DB\) và \(AB\) theo thứ tự tại \(Q\) và \(N\). Chứng minh rằng:
a) \(ABD = ACE\).
b) \(BH = CH\).
c) Tam giác \(BOC\) vuông cân.
d) \(MNPQ\) là hình vuông.
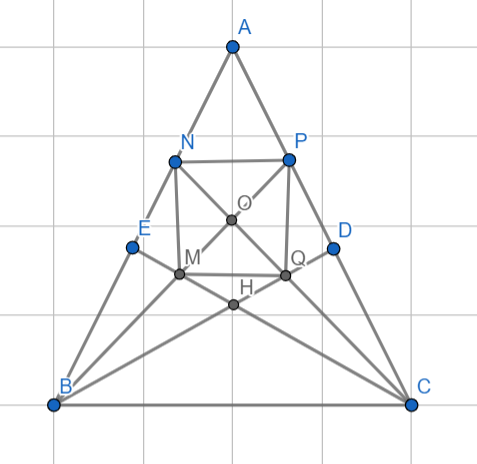
a, Xét `\triangleABD` và `\triangleACE` có:
`\hat{A}` chung
`\hat{ADB}=\hat{AEC}=(90^o)`
`=>\hat{ABD}=\hat{ACE}` `(đpcm)`
b, Ta có: `\hat{ABC}=\hat{ACB}`
`=>\hat{ABC}-\hat{ABD}=\hat{ACB}-\hat{ACE}`
`=> \hat{HBC}=\hat{HCB}`
`=> \triangleBHC` cân tại `H`
`=> HB=HC` `(đpcm)`
c, Ta có: `\hat{ABP}=\hat{PBD}=\hat{ACQ}=\hat{QCE}(=1/2 \hat{ABD}=1/2 \hat{ACE})`
`=> \hat{PBD}+\hat{HBC}=\hat{QCE}+\hat{HCB}`
`=> \hat{OBC}=\hat{OCB}`
`=> \triangleBOC` cân tại `O`
Ta có: `\hat{BOC}=180^o - (\hat{OBC} + \hat{OCB})=180^o - (\hat{OBD} + \hat{OCE} + \hat{HBC} + \hat{HCE})`
`=>\hat{BOC}=180^o - {\hat{ABD} + \hat{HBC} + \hat{HCB})`
`=180^o - (180^o - \hat{BEC})`
`=\hat{BEC}=90^o`
`=> \triangleBOC` vuông cân tại `O` `(đpcm)`
d, Xét `\triangleBMH` và `\triangleCQH` có:
`\hat{MBH}=\hat{QCH}`
`BH=CH`
`\hat{BHM}=\hat{CHQ} (\text{2 góc đối đỉnh})`
`=> \triangleBMH= \triangleCQH(g.c.g)`
`=> BM=CQ`
mà `OB=OC`
`=> OM=OQ`
`\triangleNBQ` có `BO` là đường phân giác và đường cao`=>\triangleNBQ` cân tại `B`
`=>ON=OQ`
`\triangleMCP` có `CO` là đường phân giác và đường cao `=>\triangleMCP` cân tại `C`
`=>OM=OP`
Tứ giác `MNPQ` có 2 đường chéo cắt nhau tại trung điểm mỗi đường `=>MNPQ` là hình bình hành
mà 2 đường chéo `MP=NQ` `=>MNPQ` là hình chữ nhật
mà `MP\botNQ` `=>` tứ giác `MNPQ` là hình vuông `(đpcm)`
Đúng 3
Bình luận (0)
Giúp tớ tớ vs ạ
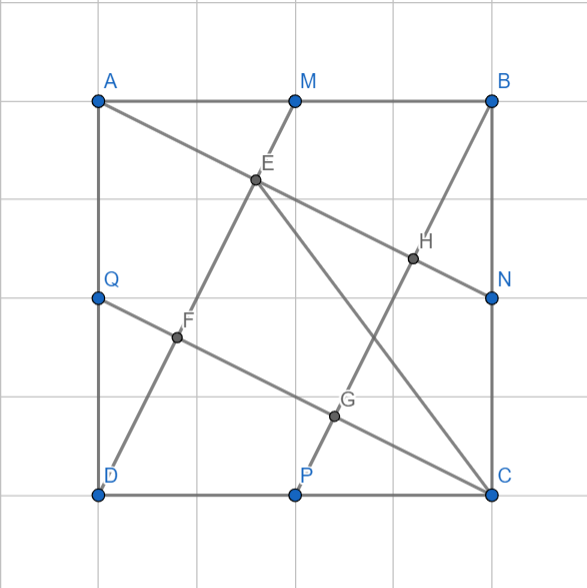
a, Xét `\triangle ANB` và `\triangle DMA` có:
`\hat{ABN}=\hat{DAM}(=90^o)`
`AB=DA`
`NB=MA=(1/2 AB)`
`=> \triangle ANB=\triangle DMA` `(\text{2 cạnh góc vuông})`
`=> {(AN=DM(đpcm)),(\hat{NAB}=\hat{MDA}):}`
Ta có: `\hat{NAB} + \hat{AME}=\hat{AME} + \hat{MDA}`
`=> 180^o - \hat{AEM} = 90^o`
`=> \hat{AEM} = 90^o`
`=> AN \bot DM (đpcm)`
b, Gọi giao điểm của `CQ` và `DM` là `F`, của `CQ` và `BP` là `G`, của `AN` và `BP` là `H`
C/minh tương tự A ta được `{(CQ\botDM),(CQ\botBP),(AN\botBP):}`
Tứ giác `EFGH` có `\hat{HEF}=\hat{EFG}=\hat{FGH}=\hat{GHE}=90^o`
`=>` Tứ giac `EFGH` là hình chữ nhật
`\triangle AEM=\triangle DFQ(ch-gn)`
`=> ME=QF`
`\triangle QFD=\triangle PGC(ch-gn)`
`=> FD=GC`
Ta có: `MD=CQ`
`=> ME+EF+FD=QF+FG+CG`
mà `ME=QF, FD=CG`
`=> EF=FG`
`=>` tứ giác `EFGH` là hình vuông
`=> DM,AN,BP,CQ` giao nhau tạo thành hình vuông `(đpcm)`
c, `\triangle DCF` có `GP//DF,CP=DP`
`=> GP` là đường trung bình của `\triangle DCF`
`=> CG=FG`
`=> EF=DF`
Xét `\triangle ECF` và `\triangle DCF` có:
`\hat{EFC}=\hat{DFC}(=90^o)`
`EF=DF`
`CF` cạnh chung
`=> \triangle ECF=\triangle DCF (\text{2 cạnh góc vuông)`
`=> CE=CD` `(đpcm)`
Đúng 2
Bình luận (0)















