a,b,c là ba số hạng của cấp số nhân

=>\(b=ak;c=ak^2\)

\(\left\{{}\begin{matrix}a+b+c=14\\abc=64\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a+ak+ak^2=14\\a\cdot ak\cdot ak^2=64\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a\left(k^2+k+1\right)=14\\a^3\cdot k^3=64\\\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}ak=4\\a=\dfrac{14}{k^2+k+1}\\\end{matrix}\right.\Leftrightarrow\dfrac{4}{k}=\dfrac{14}{k^2+k+1}\)

=>\(4k^2+4k+4-14k=0\)

=>\(4k^2-10k+4=0\)

=>\(2k^2-5k+2=0\)

=>(k-2)(2k-1)=0

=>\(\left[{}\begin{matrix}k=2\\k=\dfrac{1}{2}\end{matrix}\right.\)

TH1: k=2

\(a=\dfrac{4}{k}=\dfrac{4}{2}=2\)

\(b=2\cdot2=4;c=2\cdot2^2=8\)

TH2: k=1/2

\(a=4:k=4:\dfrac{1}{2}=8\)

\(b=8\cdot\dfrac{1}{2}=4;c=8\cdot\left(\dfrac{1}{2}\right)^2=2\)

a,b,c lập thành cấp số cộng nên a+c=2b

\(a^2+2bc=a^2+c\left(a+c\right)\)

\(=a^2+ac+c^2\)(1)

\(c^2+2ab=c^2+a\cdot2b=c^2+a\left(c+a\right)\)

\(=c^2+ac+a^2\)(2)

Từ (1),(2) suy ra \(a^2+2bc=c^2+2ab\)

Đề thiếu em, \(u_1\) bằng mấy nhỉ?

\(cos^2x=\dfrac{1}{tan^2x-1}\)

=>\(\dfrac{1}{1+tan^2x}=\dfrac{1}{tan^2x-1}\)

=>\(tan^2x+1=tan^2x-1\)

=>1=-1(vô lý)

=>\(x\in\varnothing\)

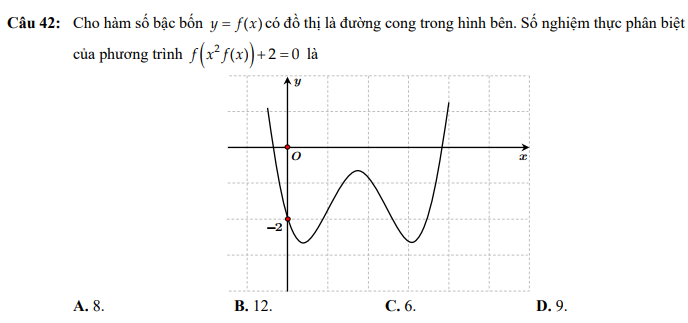
\(f\left(x^2.f\left(x\right)\right)=-2\Rightarrow\left[{}\begin{matrix}x^2.f\left(x\right)=0\\x^2.f\left(x\right)=a;b;c\\\end{matrix}\right.\)

Với \(0< a< b< c\)

Phương trình \(x^2.f\left(x\right)=0\) có 3 nghiệm

Xét \(f\left(x\right)=\dfrac{a}{x^2}\) với \(a>0\)

Đồ thị \(\dfrac{a}{x^2}\) (dễ dàng lập BBT) có 2 nhánh nằm 2 bên trục Oy, nên mỗi nhánh cắt f(x) tại 1 điểm

Do đó \(f\left(x\right)=\dfrac{a}{x^2}\) luôn có 2 nghiệm với mọi a dương

\(\Rightarrow\)Có \(3+3.2=9\) nghiệm

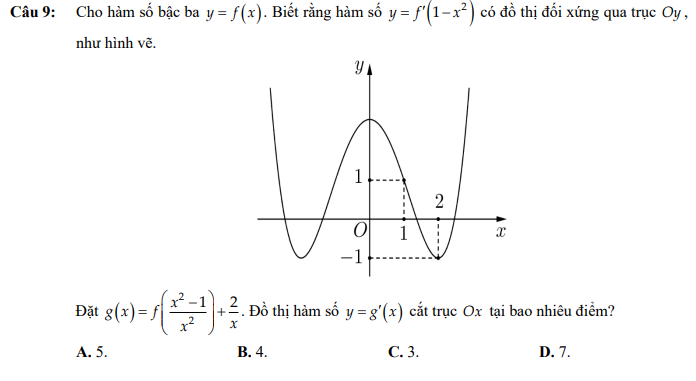
\(g\left(x\right)=f\left(1-\dfrac{1}{x^2}\right)+\dfrac{2}{x}\)

Đặt \(u=\dfrac{1}{x}\)

\(g\left(u\right)=g\left(\dfrac{1}{x}\right)=f\left(1-u^2\right)+2u\)

\(g'\left(u\right)=-2u'.\left[u.f'\left(1-u^2\right)-1\right]=0\)

\(\Rightarrow f'\left(1-u^2\right)=\dfrac{1}{u}\) (1)

Vẽ lên cùng hệ trục đồ thị \(y=\dfrac{1}{u}\Rightarrow\left(1\right)\) có 3 nghiệm: \(\left[{}\begin{matrix}u=a\in\left(0;1\right)\\u=1\\u=b>2\end{matrix}\right.\)

Ứng với mỗi giá trị u có đúng 1 giá trị x tương ứng

Nên C đúng

1.

a. Đúng

b, Đúng

c. Đúng.

d, Sai (hoặc đề in nhầm, sao còn dính x vào đây?), giá trị cot này phụ thuộc x

2.

a. Đúng, em làm  trong nháp đúng rồi

b. Sai, em làm trong nháp đúng rồi

c. Đúng, em cũng làm đúng luôn

d. Đúng, như em làm

3.

Câu này em cũng đúng hết (a là đúng)

4.

\(\dfrac{u_5}{u_2}=\dfrac{u_1.q^4}{u_1.q}=q^3=64\)

\(\Rightarrow q=4\) \(\Rightarrow u_1=\dfrac{u_2}{q}=\dfrac{1}{16}\)

Do đó:

a. Sai (đúng công bội nhưng sai số hạng đầu)

b. Sai

c. Đúng

\(u_8=u_1.q^7=\dfrac{1}{16}.4^7=1024\)

d.Sai

 \(S_{10}=\dfrac{u_1\left(1-q^{10}\right)}{1-q}=\dfrac{\dfrac{1}{16}\left(1-4^{10}\right)}{1-4}=\dfrac{349525}{16}\)

5.

a. Đúng

b. Sai

\(u_{17}=2+16.9=146\)

c. Sai

\(S_{46}=\dfrac{46.\left[2.2+45.9\right]}{2}=9407\)

d. Đúng

\(u_n=u_1+\left(n-1\right)d=2+\left(n-1\right).9=9n-7\)

1. Câu d người ta in sai đề nên em ko cần quan tâm đâu

Câu c thì đúng, 2 câu a,b em làm đúng

Câu 2 em làm đúng hết 

Bài giải